Step 1 方法起源及应用

应用领域

多项式回归法在管理学中的应用主要起源并集中于个体-环境匹配（简称P-E）研究。

因为行为交互理论表明：个体或团队态度、行为等变化的原因不能简单归因于个体或环境的因素，而应当归因于二者相互作用共同产生的效应。

方法提出

有关P-E研究的测量，主要分为两种。

第一种是直接的匹配测量。它要求被试直接判断个体与环境的匹配程度。其优点在于操作简单，但它不能考察个体或环境的独立效应。

第二种是间接的匹配测量。它要求被试分别评价个体和环境的特征，然后再对二者进行比较。常用的计算指标有：差异分数。

但是先前的间接匹配方法也存在一定的缺陷，比如使用差异分数法，当两个测量指标同时大或同时小时, 可能会得到相同的差异分数值, 而实际上测量指标本身的高、低对结果变量通常具有不同的效应。

所以Edwards和Parry (1993) 提出了的多项式回归法，来解决这个问题。

Step 2 原理说明

直线型图

首先，我们先考虑下图。

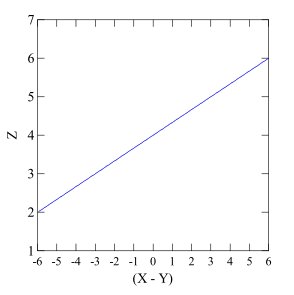
它描述了差异分数与结果的正向关系，其可由以下回归方程表示： $$ Z=b_0+b_1(X-Y)+e. $$ 其中：Z是结果；X是个体；Y是环境；e是随机误差。

将上式展开可得： $$ Z=b_0+b_1X-b_1Y+e. $$ 结果如下图所示：

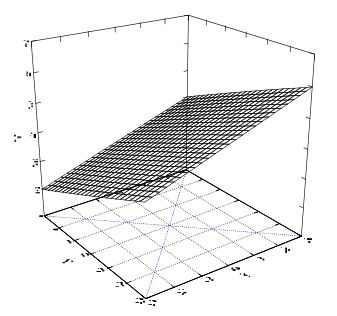
其中X和Y的系数受到了约束，即限制了个体和环境对结果的作用相同。但往往现实并非如此，所以将上式的约束条件放开，可得下式： $$ Z=b_0+b_1X+b_2Y+e. $$

倒V型图

接下来，我们考虑倒V型图。

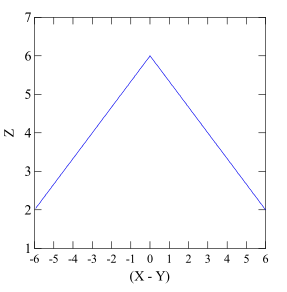
如图所示，当X与Y相等时，结果最大化，即可由以下回归方程表示： $$ Z=b_0+b_1\lvert X-Y\rvert+e. $$ 但是，因为绝对值没办法被展开，所以将上式替换为： $$ Z=b_0+b_1(1-2W)(X-Y)+e. $$ 其中W是一个潜在变量，当X-Y为正时等于0；当X-Y为负时等于1；当X=Y时随机为0或1。将上式展开可得： $$ Z=b_0+b_1X-b_1Y-2b_1WX+2b_1WY +e. $$ 结果如下图所示：

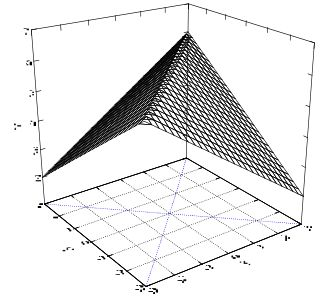
但是其中X和Y的系数依然受到了约束，所以将上式的约束条件放开，可得下式： $$ Z=b_0+b_1X+b_2Y+b_3W+b_4WX+b_5WY+e. $$

倒U型图

最后，我们考虑下图。

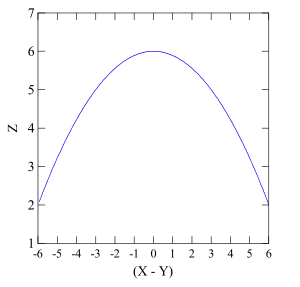
它与倒V型图相似，但其上升和下降幅度存在差异。这两类图形所示关系在P-E研究中较为常见，其可由以下回归方程表示： $$ Z=b_0+b_1(X-Y)^2+e. $$ 将上式展开可得： $$ Z=b_0+b_1X^2-2b_1XY+b_1Y^2 +e. $$ 结果如下图所示：

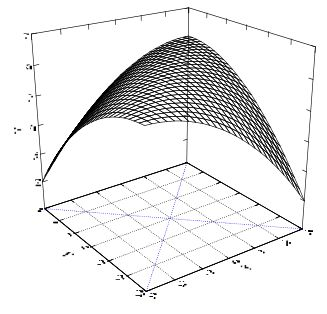
其中 X2、XY、Y2的系数依然受到了约束，所以将上式的约束条件放开，可得下式： $$ Z=b_0+b_1X+b_2Y+b_3X^2+b_4XY+b_5Y^2+e. $$ 注：放开约束条件后，在展开过程中，当X乘以Y和Y乘以X时，不能简单的将结果合并为XY；而应该将其转化在X、Y、XY三个因子上。

公式10就是多项式回归中常用的范式了。大概说到这一步，原理解释部分就可以告一段落。接下来就是数据分析的部分。

数据分析部分的操作简单，只要在SPSS中做出中心化的X、Y、X2、XY、Y2这几个项，随后用线性回归的方法算出b1-b5的取值与显著性即可。

关于多项式回归的难点在于对数据的结果进行解读。现阶段的萜妹，自我感觉只是勉强一只脚入了门，所以还有很多需要学习的地方，下一次推送估计只能讲解最简单的解读方法啦~

另外，如果有小可爱对这种方法有兴趣，可以多看看Edwards的文章，尤其推荐Polynomial Regression and Response Surface Methodology，这篇推送差不多就是基于这篇2007年的文章的哟~

外文文献的下载方法可以看之前的文章，那么今天的推送就到这里了~

小可爱们，下周见~

原文推送：

➪干货丨多项式回归之原理篇

RSA丨多项式回归之原理篇