RSA丨多项式回归之操作篇
啦啦啦啦啦,在一次又一次提笔失败后,萜妹终于鼓起勇气来填我欠下的各种坑了,先从最近的开始补,所以今天先手把手教小可爱们多项式回归的操作啦~
以下的操作以论文写作的顺序来进行。
话不多说,我们直接开始。
(注:原理篇在很久前的一篇推送里,大家有兴趣可以去菜单里查看。)
Step 1 分析策略
分析策略这个部分是通常论文写作中不会单独列出的部分,但是在多项式回归与响应面分析中,这块内容会在研究方法的最后部分被提及。
接下来,萜妹介绍一下分析策略这部分的写作范式。因为是根据萜妹自己看文章总结出来的,所以个人认为是可以这么写,而不是说一定要这么写哈。
模型构建
首先要用多项式回归的方法构建构建模型,写明公式及公式内各项内容的代表意义。
需要注意的是,有的时候数据具有嵌套性,所以会使用多层线性模型(HLM)进行假设检验,这种情况下公式要变形成两层。
萜妹这里就只列举最最传统的公式给大家参考,各种变式也是在这个基础上得来的。 $$ M=b_0+b_1L+b_2T+b_3L^2+b_4(LT)+b_5T^2+e $$
其中L、T是需要进行一致性检验的变量,M是多项式回归的目标变量,这三个字母不固定,可依研究的具体内容而设定。
假设说明
这个部分的写作目的是为了说明如果要满足预先的假设,数据应该呈现出一个怎样的结果。这个部分要对照假设一条条写,而之后的结果部分也会对照这里提出的条件来挨个验证是否都满足。
接下来萜妹会对几个常用的例子进行具体说明,希望可以帮助小可爱们理解条件存在的意义。
H1:L与T一致性越高,M取值越大。
若要假设成立,需要曲率显著以保证拐点的存在,而不是呈线性关系;而曲率为负说明拐点值取到最大值,如果假设一致性高,M取值越小的话,此时曲率为正才能符合假设。此外,对于凹曲面而言,第一主轴为向下曲率最小的直线,即是凹曲面的脊投射与LT平面的直线,因此如果要满足假设,第一主轴与与一致性线不能产生偏移。
因此,假设成立需要满足的条件:
①不一致性线*(L=-T)*上 ,曲率为负且显著;
②第一主轴没有偏离一致性线*(L=T)*,即斜率 p 11=1、截距p10=0。
H2:在一致性情况下,与双低相比,双高对M的影响更大。
若要满足假设,需要一致性线呈简单线性关系,因此曲率不能显著;此外斜率为正说明双高比双低的正向效果显著;若假设相反,则需斜率为负。
因此,假设成立需要满足的条件:
①一致性线*(L=T)*上 ,斜率为正且显著;
②一致性线(L=T)上 ,曲率不显著。
H3:在不一致性情况下,与“低T高L”相比,“高T低L”时M取值下降的更快。
在不一致性线上,M的下降速率取决于各点的斜率(注:这和我们上文之前提到的斜率不一样哈),所以为了求得斜率表达式,我们要对不一致性线求导,结果为斜率=a3+2a4X,所以斜率为0时,拐点的横坐标=-a3/2a4,。若要满足我们的假设,拐点应该小于0,这样在正半轴下降速率会高于负半轴;若假设相反,则拐点横坐标需大于0.
因此,假设成立需要满足的条件:侧偏移量-a3/2a4取值为负。
H4:中介与调节作用
有关中介与调节的检验与传统方法大致相同,区别的是需要先构建一个块变量代表T与L的一致性效应。具体构造方法就将已算出的b0-b5代入最开始的公式就好啦。
Step 2 实际操作
就萜妹个人而言哇,我是觉得多项式回归难就难在理解上,其实操作上还是比较简单的,所以在下面的过程中,萜妹以前介绍过的操作就不附图说明啦,更多的可能是告诉小可爱们,我的一些经验和要注意的地方。
计算b0-b5
其实计算b0-b5是一个非常简单的过程。我们只需要在SPSS里做一个简单的回归就好。
具体操作:
①自变量标准化或者中心化;
②在SPSS的计算变量中完成自变量的平方项和交互项的生成过程;
③在SPSS中进行回归分析。目标变量是我们的结果变量,而对其有影响的变量包括控制变量、自变量、自变量的平方项和之间交互项。
此外,多项式回归的数据处理第一个需要注意的点是,一般我们做数据分析时用的都是标准化的分数,但是多项式回归这里,因为T、L二者的量表拥有的是相同的度量标准,因此我们*对自变量只***进行中心化也可以。当然,要还是想用标准化当然可以用标准化的了。
第二个需要注意的地方是:在进行回归时,**结果变量不要选择标准化的数据,**因为这样会使截距消失,通常情况下多项式回归的响应面分析图都是有截距的。至于控制变量进不进行标准化,这个就看个人选择了,个人觉得影响不大。
计算a1-a4
根据回归得到的b0-b5可以根据公式很轻易的算出a1-a4,之后可以根据EXCEL算出它们的显著性。
具体操作:
①根据Shanock(2010)文章里的协方差计算语句在SPSS里计算出自变量及其平方项和交互项的协方差;

②在polynomial regression tool的EXCEL文件里,根据SPSS求得的数据把下图中白色部分填充完整。
③之后EXCEL中下图部分就会自动计算完成,可判断a1-a4的显著性。
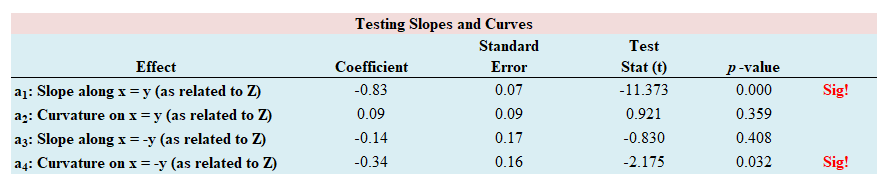
需要注意的是第二步里头,非标准化系数后一列是标准误哈,萜妹有次输成了标准化系数(因为SPSS结果里头,标准化系数那一列正好第一行是空的),结果愣生生试了半个多小时怎么算都算不出显著,恩,可以说是自己把自己蠢哭了。
计算X0、Y0、P10、P11、P20、P21
这一步也是完全依靠EXCEL的傻瓜操作呀。不过这里的指标不是都需要看,主要是p10和p11。而且这两个指标的显著性,萜妹还不会直接计算,不过好险找到篇文章里有P11=1的95%置信区间为[-3.73,6.05];P10=0的95%置信区间为[-0.09,2.32]。所以小可爱们只要把计算出来的值和上述区间作比较就可以啦。在区间范围内就是不显著,没有偏移。
具体操作:
①在surface的EXCEL文件里输入b0-b5;
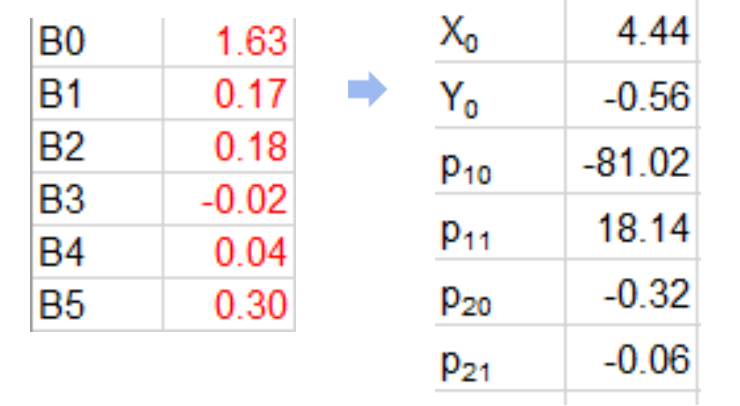
②EXCEL会自动计算出右图部分。
制表
计算完上面所有内容后,就可以制表撰写H1-3的证明部分了。证明部分这个就结合之前的分析策略写就好,表格的话,萜妹找了个范例,不过小可爱们也可以根据假设自己调整要汇报的内容哇~
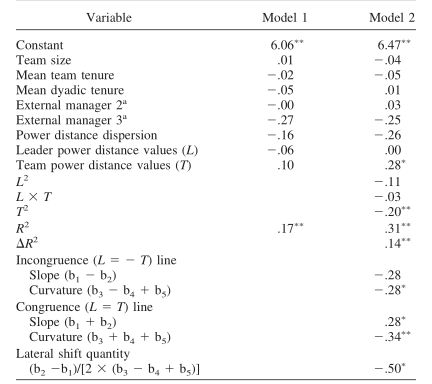
计算块变量
如果涉及到中介和调节变量的话,我们需要利用SPSS构建块变量再进行分析,块变量的构建方法也很简单粗暴。就直接在SPSS的计算变量里按照公式输入就好,要记得数字和变量的乘积需要在二者间输入*哟,不然SPSS会判定错误的~
生成块变量后,大家就按正常的分析就好,需要注意的是这个时候的计算就全部用标准化系数了哈~
啦啦啦,文章写到这里就差不多结束啦,和通常论文写作一样的步骤,萜妹这里就都跳过了,毕竟我们的重点是多项式回归嘛。
之后,还想说的是,萜妹我是写到一半才想起来,我好像还没有介绍过拐点、主轴、一致性/不一致性线的,啊,当下是非常崩溃的,但是那个介绍部分再加到这一篇里,内容肯定超了。
所以我还是先把这篇写出来了,大家要是对那些特点弄不清楚的,萜妹看反馈,到时候再补一篇说明好了。
小可爱们,下周见~
原文推送:
