QCA丨基础篇
啦啦啦,这是一个新的笔记系列,内容源于李永发教授的方法论坛。这次大概会和2017重庆系列一样,算是一个大专题,希望小可爱们读完这个专题后,都会操作QCA哟~
之后,为了让小可爱们更能接受,萜妹对介绍内容按照我自己的思维习惯进行了逻辑调整(我也不能保证调整完的逻辑更好),所以小可爱们如果有觉得看的迷茫的地方可以跟我沟通吼~
用途
QCA回答的关键问题是:导致某一个现象(结果)发生的前因条件什么?不发生的前因条件是什么?导致结果发生条件的个数是否可以减少?促使某一个现象(结果)发生的充分条件什么?必要条件是什么?
注:萜妹认为QCA的本质也是寻找因果关系。只不过比起案例分析,它更加客观;比起传统线性回归,它更能清晰体现因果的复杂性。
结果
做QCA,萜妹觉得最重要的就是能操作软件并把结果图画出来,所以萜妹从结果图说起,先带小可爱们认识这个图。
注:结果的表现形式有多种,萜妹这里采用的是QCA领域里头的大牛FISS(2011)的标准。
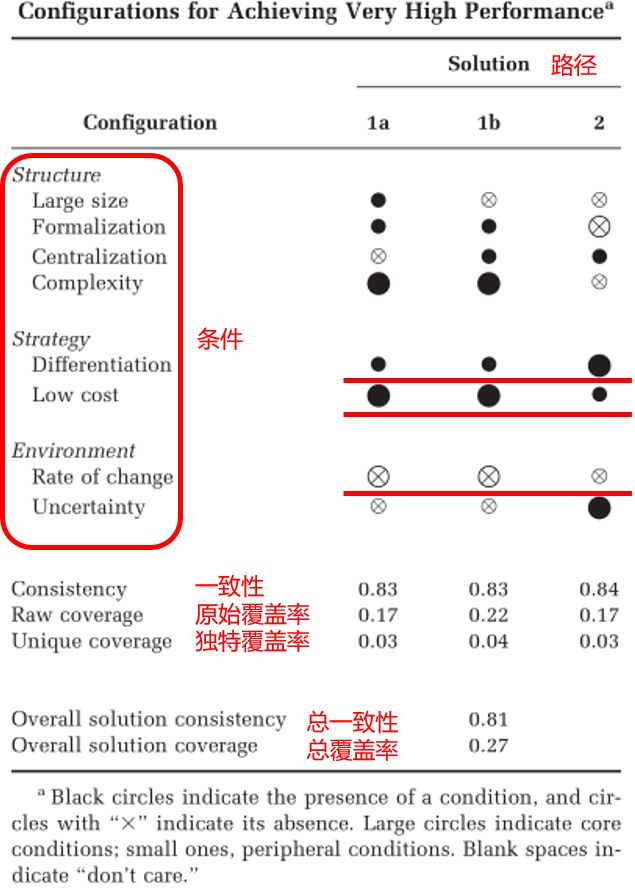
首先,从这个图就能看出来QCA和与线性回归不同在于:自变量与因变量并非同增同减。如图:公司规模大这一条件出现与不出现都有可能导致高绩效。
其次,结合上图解释一下充分条件与必要条件。
- 右边的每一个纵列代表一个路径,即一组解,而每一组解都是现象发生的充分条件;
- 右边标红的横行中条件在每个路径中的状态相同,则说明这是必要条件。注:上图中变化率的不出现也是高绩效的必要条件,所以只要状态相同,不论是出现还是不出现都是必要条件。
条件表述有5种可能,分别为●、⚫、⊗、(大⊗)和(空)。
(注:大×和空,萜妹在这里打不出来,所以大家意会一下。)
- ⊗表示该条件不出现,●表示该条件出现;
- 空表示不对结果产生影响,上图中并没有;
- 大的是核心条件,即简单解;小的是外围条件,即中间解,**注:二者在重要性上并没有差别!!!(一定不能有误解)。**简单解和中间解的区别会在之后的推送中论述。
核心概念
QCA有一些核心概念,需要小可爱们了解,这里萜妹就先把定义写出来,具体解释和深度的内容,我们之后在案例篇详细说。
- 一致性:解的可靠性;
- 覆盖率:覆盖案例度;
- 组态:给定结果相关的条件属性的组合(注意这里是不包括结果值的)。
特征
QCA具有三大特征分别为:
- 非对称性(条件与结果非同增同减);
- 等效性(条条道路通罗马,路径不随出现概率而改变重要性。如,普通高考与自主招生都是进入大学的途径,其重要性相同);
- 因果复杂性(如字面意思,不解释)。
类型
目前QCA主要分为三类。
| 类型 | 名称 | 变量范围 | 变量值格式 |
|---|---|---|---|
| csQCA | Crisp-set | 清晰集 | 二元的present(1)和absent(0) |
| mvQCA | Multi-value | 多值集 | 多元的离散的数字:0,1,2,3,4 |
| fsQCA | Fuzzy-set | 模糊集 | 连续的0~1之间精细的刻度值 |
注:①多值集需从0开始取值,最多取到4,软件无法计算更大的值。二元是只取到1的多元,所以能分析mvQCA的都能分析csQCA;
②模糊值是指多大程度属于xx条件,如:多大程度觉得自己属于高收入群体。清晰集只取0和1,也是模糊集的子集。
操作说明
首先需要明确一点:*因果关系与背景和并发特性有关,因而QCA***拒绝任何永久性因果关系的形式。
换句话说,所有的QCA都是有限制的,限制条件主要体现在背景和维度(并发特征)选择上,所以QCA的前提是需要先控制背景并选定维度。
之后,QCA操作的前期准备操作包括:①找结果变量(有趣且有意义);②梳理前因/条件(可从已有文献或者理论中获得);③寻找案例。
样本选择
样本选择主要有两个方面需要注意,分别是选择原则和选择数量。
一、选择原则
①案例是构建的而非随机选取的。
②案例选择需要尽量覆盖所有情况,但是无法强求一定实现全覆盖。
二、选择数量
样本与建议数量的对应关系如下图所示:
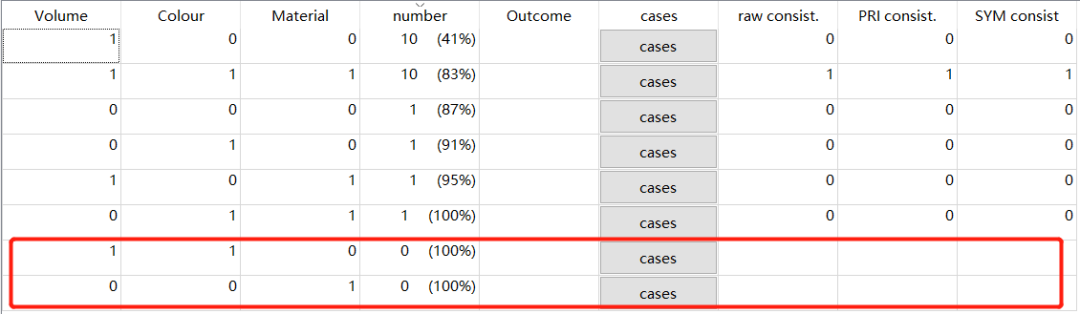
在中等样本分析(10~40个案例中),通常选择4到6/7个解释条件。
不过也有样本数只要大于2的k-1次方就好的说法,k代表维度个数,如3维条件,那么4个案例就可以了。
但是无论是那种选择标准,都是可进行QCA的最小值。如果实际情况中,限定背景后仍有40个案例,还是不能只选满足最小值数量的案例,应该需要全部纳入。
啦啦啦,QCA的基础介绍到这里就先告一段落了。接下来的一篇是软件操作介绍。小可爱们,我们下周见吧~
原文链接:
