QCA丨进阶篇 ( 重难点 )
啦啦啦,这篇推送终于要填补之前留下的概念坑啦~
由于干干的说怕小可爱们理解不了,所以萜妹这次会依托于上周介绍的抽球问题的衍生案例,逐一给大家介绍哇~(PS:这一篇将用到软件篇中的很多内容,建议小可爱们在掌握软件后查看!)
原始案例
考虑到小可爱们可能不记得萜妹上一篇的内容了,所以这里再把抽球问题的原始案例复述一下。
假定 :
- 体积 :大为1;小为0
- 颜色 :红为1;白为0
- 材质 :钢为1;玻璃为0
- 结果 :中奖为1;没中奖为0
求解目标:
促使结果发生的简约条件。
注:接下来的进阶案例中维度设定和求解目标与原始案例相同,就不再反复说明啦~
案例分布:
考虑到之后案例数据会比较多,所以数据的呈现方式有所改变,不再是原始数据的截图了哟,不过分享的文件里头还是有各案例原始数据的Excel吼~
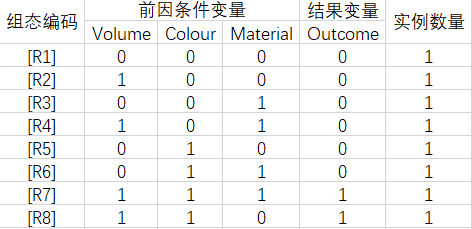
真值表:
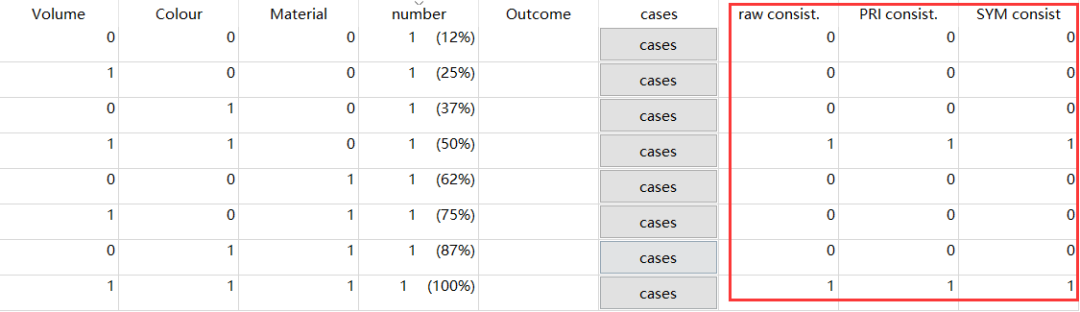
萜妹认为QCA软件的运算过程,都是从原始数据得真值表,再由真值表求解,所以真值表至关重要,于是萜妹把原始案例的真值表也截过来了,方便小可爱们跟之后的案例进行对比。
注:真值表前半部分是描述性统计,真正影响求解结果的是后半部分(红框中内容),因为红框中内容会因为设定值而影响outcome列,进而影响结果。
求解结果:

原始案例的求解结果中:复杂解、简单解和中间解都一样,QCA中看中间解最好(原因在之后的案例会说),所以萜妹就只截了中间解。
至于原始案例的求解操作,在软件篇中有详细说明,萜妹就不复述了。
进阶案例1
该案例需要说明的问题是:案例选择时,扩大某一组态中的案例数量,对结果没有影响。
案例分布:
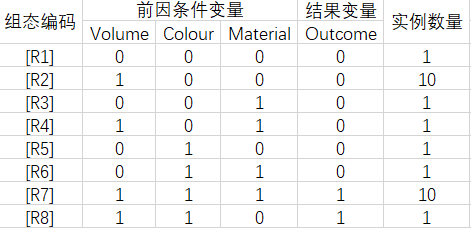
可以看出,这与原始案例的区别在于:有两种组态的数量得到了增加。
真值表:
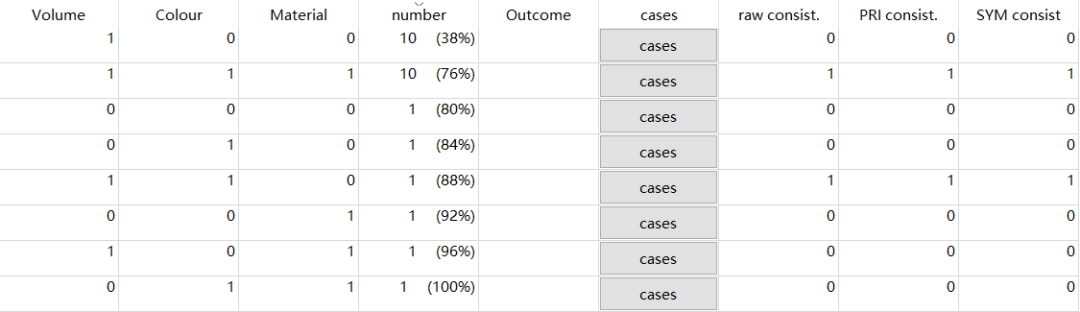
之后,进行数据操作,可以发现:进阶案例1与原始案例的真值表只在描述性部分有差别,分析部分完全相同啊!!!
求解结果:

结果就是:二者的求解结果也完全一样啊!
所以小可爱们,在用QCA处理问题的时候,同一组态内,案例数是1还是100,对结果根本没有任何影响!!!那么,·我们为什么还要去收集尽量多的案例呢?进阶案例2会给你们答案~
进阶案例2:矛盾组态
收过问卷的小可爱们肯定都知道,有时候问卷的质量难以保证,所以我们希望尽可能多的收集数据。
但数据的增多常常会出现两个被试的自变量选择相同,而结果变量选择完全相反的情况,那么这种时候,该信哪一种呢?
当然,这种情况在问卷收集中太稀疏平常了,所以通常都是软件处理,我们不会太去在意。但是QCA这种研究方法则注意到了这种情况,并将这种情况下的条件变量合集命名为了矛盾组态。
这么说可能小可爱们还没完全清楚,萜妹用进阶案例2让大家直观感受。
案例分布:
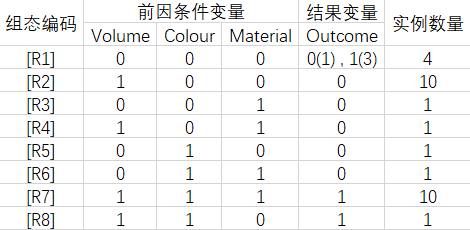
可以看出,这与进阶案例1的区别在于:组态[R1]是矛盾组态,结果变量出现了两种情况。
真值表:
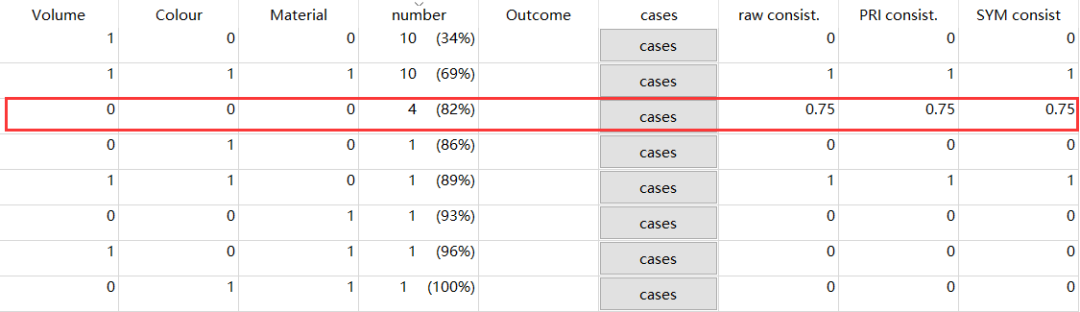
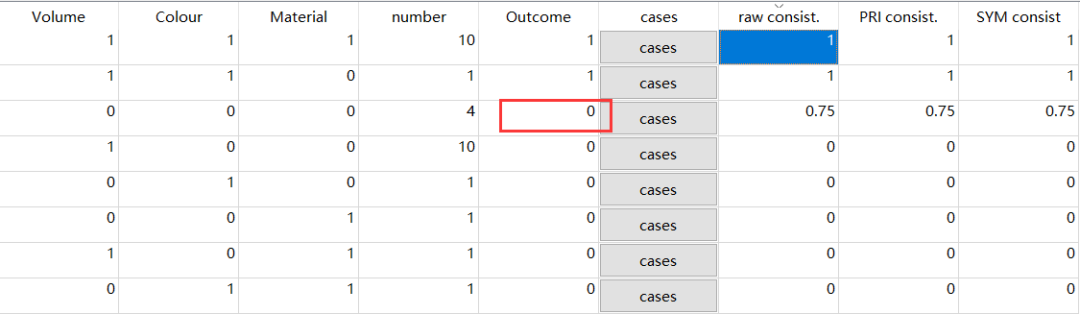
小可爱们可以看到,这里的真值表与上面有了明显的差别:组态的一致率不再都是1,出现了一个0.75。
点开0.75这一行的【case】,可得:
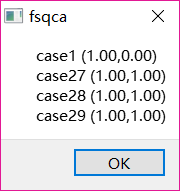
注:name(1,x)中:name是案例名;整个符号的意义是在这个案例中如果自变量或自变量组取1,结果变量取x。用人话说:
- name(1,1)代表自变量正,结果变量就正;
- name(1,0)代表自变量正,结果变量就负。
看到案例的显示,小可爱们应该就能理解这里的一致性为什么是0.75了吧。
这里的一致性=符合结果的案例数/该组态总案例数
注:如果是求结果不发生的情况,则三正一负的一致性则是0.25。
求解过程:
矛盾组态存在,有助于我们软件篇里的一些遗留问题的解决,所以进阶案例2的求解过程,萜妹会适当截图。
上周我们说过,下一步的【Delete and code】的过程,我们通常取默认值,即1和0.8。
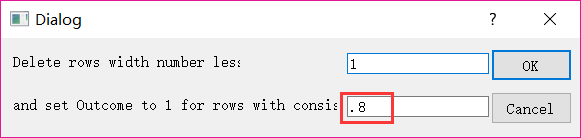
【OK】后,会得以下结果,注意红框部分。
这与原始案例点击【OK】后的结果一样,所以结果也和原始案例一样。(可参照进阶案例1就不截图了)
那么,我们尝试将这个0.8修改成0.75会如何呢?
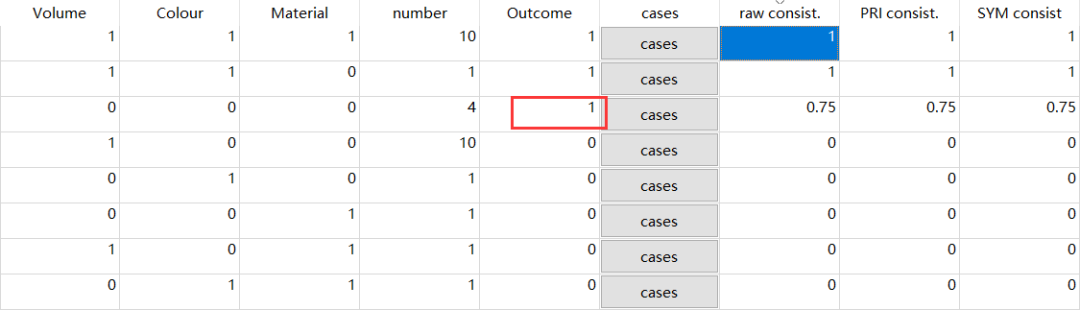
可以发现,真值表明显与之前有所不同。
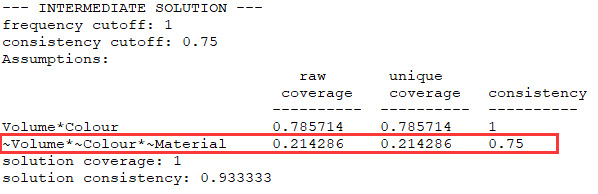
最终结果相较于之前,也明显多了一条路径。
通过这个案例,小可爱们可以更深刻的理解【Delete and code】中的第二个空代表着:一致性达X才被软件接受。
进阶案例3:逻辑余项
介绍进阶案例3之前,萜妹想先让小可爱们理解,什么是逻辑余项,从概念上说:逻辑余项是在现实生活中存在,但是无法获得数据的情况。
数据收集的过程中,逻辑余项出现的可能性非常高,那么这种情况下如何进行数据分析呢?萜妹用进阶案例3给小可爱们简单演示。
案例分布:
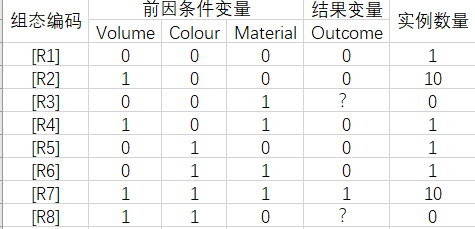
可以看出,这与进阶案例1的区别在于:组态[R3]和[R8]未收集到数据,不知道结果情况。
真值表:
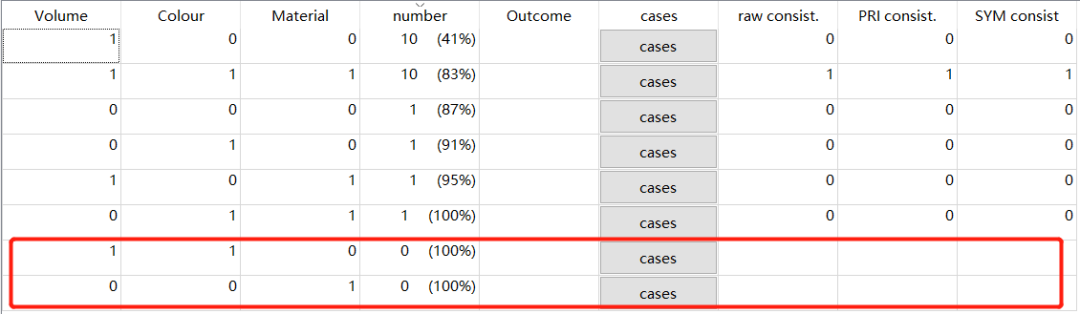
可以看到这里的真值表显示了逻辑余项的存在。
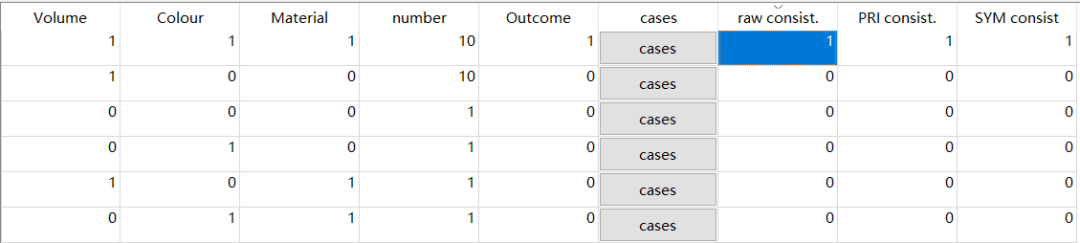
【Delete and code】操作后,真值表有所改变:outcome出现数值,且逻辑余项消失。
求解结果:
逻辑余项的存在并不会影响小可爱们使用fsQCA3.0的软件操作,所以这里就不再细说。
由于进阶案例3的结果不再是复杂解、中间解和简单解全部一样,所以这里萜妹把三个解都进行了截图。
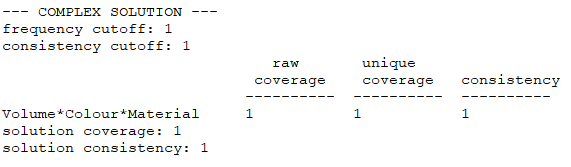
复杂解(COMPLEX SOLUTION)

简单解(PARSIMONIOUS SOLUTION)
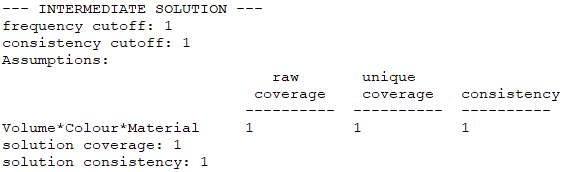
中间解(INTERMEDIATE SOLUTION)
复杂解、中间解与简单解
这三种解的类型萜妹已经说过多次啦,fsQCA3.0的运算结果会直接得到这三种解,那么为什么加入逻辑余项后三者不同?它们各自的特点又是什么呢?
软件逻辑:
在细说区别之前,我们首先要明白,使用QCA的目的是什么。
萜妹理解的目的就是找到简约条件。
举个不恰当的小例子:平衡积分卡需要从财务、客户、运营和学习成长四个角度进行评价,以提高企业绩效。而我们在使用QCA后可能会发现,四者不一定需要同时存在,满足某三个或者某两个角度的组合就可以实现高绩效。那么结果的各个路径就是我们的简约条件。
这种思想体现在数据分析中,就表现为:软件运作时会朝着不断降维的方向努力。
反事实假设:(重难点!!!)
在明白软件逻辑后,我们还需明白这种努力是如何被实现的,于是又引入一个概念:反事实假设。
因为事实中并没有逻辑余项对应组态的数据,所以软件在运行过程中,会根据其他数据对该部分进行赋值。但是无论赋值多少,这都是与现实不符的,因此软件的这种行为被称为反事实假设。
反事实假设可分为两种:
-
“简单”反事实:将一个冗余的因果条件添加到能促使结果发生的因果条件中;
比如:已知A*B*~C是一组因果条件,且由理论和实践推出A*B*C大概率也是因果条件,那么我们可将ABC这个冗杂的因果条件加入AB~C中,因此可得到A*B是因果条件的结论。这整个推论过程是较为容易的。
-
“困难”反事实:在假设某一条件是多余的情况下,将某一条件从能促使结果发生的因果条件中移除。
比如:已知A*B*C是一组因果条件,但由理论和实践无法推出A*B*~C大概率也是因果条件,那么我们想要假设ABC中的C条件是多余的,进而将其移除,得到A*B是因果条件的结论。这整个推论过程是较为困难的。
(注:以上是萜妹自己的理解和翻译,原文在资料包里的文献中,还是FISS(2011)的那篇,小可爱们感兴趣可以自己去看)
以上是官方说法,讲道理,乍一看萜妹我是没看懂的,所以我结合自己理解跟大家说说人话。以下是萜妹自己的理解。
- “简单”反事实假设是有把握的约简;
- “困难”反事实假设是有风险的约简。
至于有把握和有风险的界限在哪,这是软件处理中的黑箱部分,萜妹也没办法给出答案。我觉得理解了定义就行,不要太纠结在这里。
各解区别:
小可爱们确保已经能分清“简单”反事实假设和“困难”反事实假设后,这三种解的区别就很好理解了。
- 复杂解:是不考虑逻辑余项的情况;
- 中间解:是只考虑“简单”反事实假设的情况;
- 简单解:是既考虑“简单”反事实假设,又考虑“复杂”反事实假设的情况。
那么,中间解比复杂解更简约,又比简单解更可靠,所以它才是最优解。
Tosmana软件补充
前面所有的示范都是用的fsQCA3.0,所以萜妹这里再写一个Tosmana软件在处理矛盾组态和逻辑余项的补充说明。
前面的步骤软件篇都讲过,这里就都跳过了,直接到求解这里。
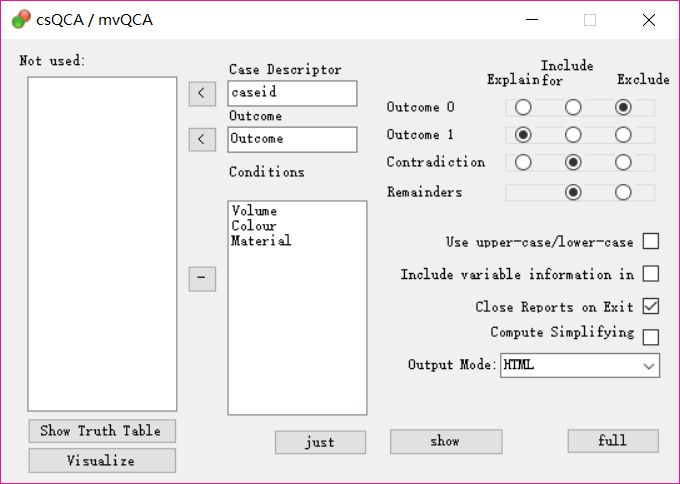
【Contradiction】为是否考虑矛盾组态;【Remainders】为是否考虑逻辑余项。(上图二者均选是)
当【Contradiction】选择否时,则出现矛盾的组态所有数据被软件无视,该组态将被当做逻辑余项进行处理。
当【Remainders】选择否时,求解结果为复杂解;当【Remainders】选择是时,求解结果为简单解。
这一篇推送,萜妹觉得是QCA里最难的部分了。反事实假设在听讲座的时候就把很多同学绕晕了,萜妹好不容易才理解了,但是我的语言有没有让小可爱们也能理解,这我也不确定。小可爱们要是理解不了,可以再和萜妹沟通,或者就强行记住中间解是最优解的这个结论吧,反正原理并不影响大家的软件操作啊~
之后,上次有小可爱问我具体怎么操作,所以萜妹决定下周推送写个完完整整的示范案例,从案例的选择到最后图表的形成。
那小可爱们,我们下周见啦~
原文链接:
