跨层次的被调节的中介
该篇推送主要介绍跨层次的被调节的中介,该类型模型较多,推送中以跨层次的第一阶段的被调节的中介模型为例,具体内容包括:
模型介绍
跨层次的被调节的中介还是有多种类型的。讲座中着重分享的是跨层次的第一阶段的被调节的中介模型,所以接下来萜妹也会以这个为例,具体模型如下:
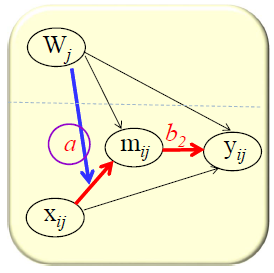
跨层次的第一阶段的被调节的中介模型
模型公式
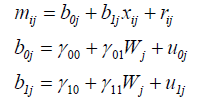
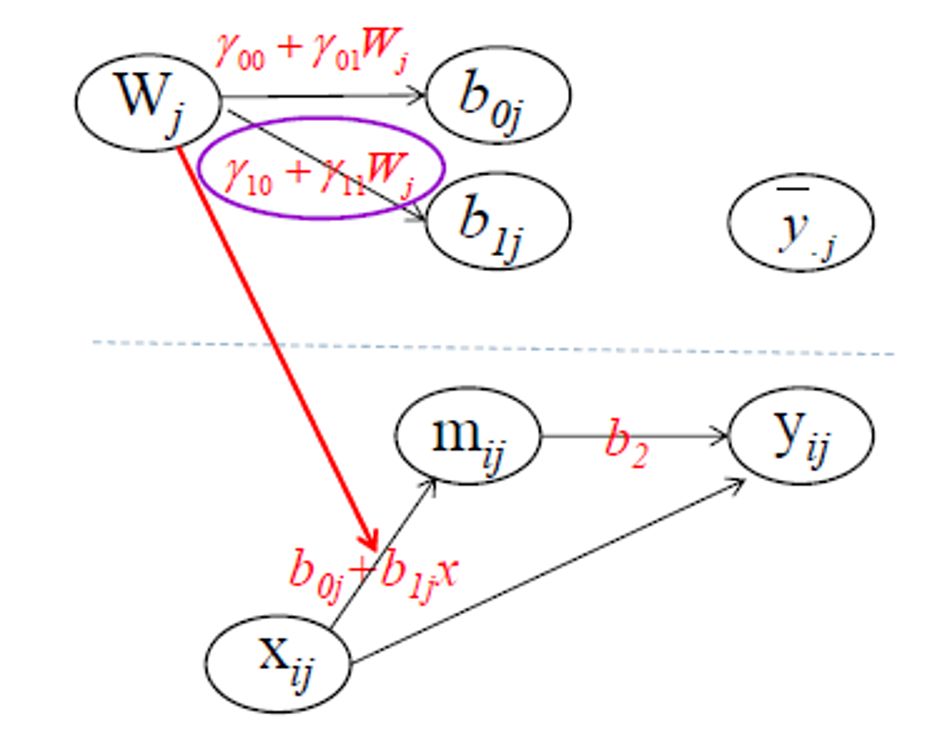
成立条件
回顾单层的第一阶段的被调节的中介模型,它的成立条件是 (a1+a3×W)×b2 随着W的取值将有显著差异。
那么我们类比一下,b2的部分其实是没有变化的,所以b2还是b2,那前面的(a1+a3W)在这个模型里变成了什么呢?
这就要求小可爱们先要弄清楚(a1+a3W)的意义了,(a1+a3W)其实代表的是x对m斜率的影响,我们这里(γ10+γ11×Wj)代表的才是斜率,所以本模型成立条件为 (γ10+γ11×Wj)×b2 随着W的取值将有显著差异。
(斜率这种说法在单层的时候可能没有那么准确,但是小可爱们仔细把两个公式放在一起对比的话,应该能理解萜妹的意思的。)
补充说明
这里额外要注意的两点是:
- 第一,为什么模型中额外画出了level2的y?因为总⽅方差既有组间⼜有组内,然而我们只研究的是组内部分。但是涉及跨层时,软件默认会拆开因变量。
- 第二,最好加上变量间的相关关系。虽然加相关会降低主效应,但是可以提⾼高模型拟合度。
Mplus语句
TITLE: A two-level first-stage MoMe;
DATA; FILE IS example.txt;
VARIABLE: NAMES ARE x m w y cluster;
USE VARIABLES ARE x m w y;
CENTERING IS GRANDMEAN(w) ;
CENTERING IS GROUPMEAN(x) ;
CLUSTER = cluster;
WITHIN = x;
BETWEEN = w;
! x、w是外生变量,需要自己定义;m、y是因变量,又是内生变量,会自动拆分。
ANALYSIS:TYPE=TWOLEYEL RANDOM;
MODEL:
%WITHIN%
S | m on x;
y on m (b2)
x;
% BETWEEN%
S on w (a1) ;! γ11
[ S ] ( a0 );! γ10
m on w;
m with S;
y with m;
y with S;
y with w;! 相关
MODEL CONSTRAINT:
NEW (w0 ind_h ind_l diff) ;
w0=0.85;
ind_h=(a0+a1*w0)*b2;
ind_l=(a0-a1*w0)*b2;
Diff = ind_h - ind_l;
OUTPUT:
SAMPSTAT;
CINTERVAL;
补充分析
由于Mplus不能做跨层次的Bootstrapping,所以需要用parametric bootstrapping解决上述问题。
原理:回归系数的抽样分布为t-test,所以a、b都是t分布,即都是可以通过随机抽样得到的。因此单纯抽取出一组a、b相乘得一个ab,重复10000次就可以得到最终的ab分布图。
缺陷:然而这里将出现的一个新问题是,parametric bootstrapping需要用R语句做,emm……萜妹没研究过R,也没什么其他的心得,所以小可爱们要使用的话就直接看讲座资料好啦!
模型结果
ppt上并没有给出上述语句的结果,但是应该和之前的大同小异,所以这里也不复述啦~
啦啦啦,跨层次的被调节的中介就介绍到这里啦,其实萜妹也知道这种模型只是其中的一个小小个例,但是萜妹我自己也不敢发散太多,毕竟把握度没有那么大,所以还是先这样告一段落啦。
之后,下周应该是跨层次的被中介的调节模型,萜妹还没想好是分两次写还是合一起写。不过,看小可爱们对这个系列的兴趣已经不太大了,所以很有可能做一次更了,尽快把这个系列结束,再带小可爱们看新东西吧~
我们下周再见啦~
原文链接:
