数据分析部分萜妹希望能用通俗的语言，帮助小可爱们搭建数据分析的框架，并且告诉小可爱们要做成什么样，为什么要这么做，以及怎么做。

萜妹把需要做的数据分析分为了三个大类，分别是：数据有效性分析、样本基本描述、数据具体分析。

数据有效性分析：信度检验、验证性因子分析、共同方法偏差检验。
样本基础描述：描述性分析、相关分析。
数据具体分析：回归分析、bootstrap法、简单斜率分析（涉及调节时使用）。

注：以上为至少要完成的操作，面对特殊情况的额外操作，这里未提及。如无特殊情况，完成上述操作即可。

接着上周的内容，我们这周进入数据具体分析的部分，那我们开始吧~

假设分析是文章数据分析部分的重头戏，所以相比于前两个部分，这个部分萜妹还会进行二次分解，最起码有基础概念、常见模型、视频演示和进阶模型，尽我最大可能让大家能看懂吧。

其实具体的操作，萜妹的笔记系列都有过详细介绍。但是小白，通常还是云里雾里，所以这次萜妹想在操作之前用我自己的话，跟大家说一遍基础性的概念和原理~

以下会详细介绍的原理有：调节与中介，另外也会结合着介绍一些常见的概念，比如：显著性、中心化/标准化、部分中介/完全中介。

调节效应

【模型】

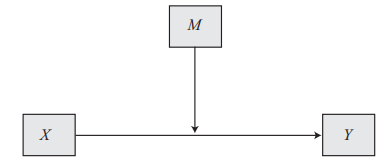
注：X是自变量，Y是结果变量，M是调节变量。

【定义】

官方定义：如果两个变量之间的关系（如Y与X的关系）是变量M的函数，称M为调节变量。

萜妹理解：就是X和Y的关系会随M的取值而有所不同（这说的不一定有定义清楚），萜妹还是举些例子来加深理解吧（以下例子基于常识，萜妹未进行科学考证，重点是帮助理解什么是调节，实际情况不一定对！！！）。

喝牛奶(X)有利于长高(Y)，但是对于10岁和70岁效果不同，此时年龄就是调节变量(M)。
女生看到帅哥会开心，但男生不会。那么看帅哥是X，开心是Y，性别是M。

【数理解释】

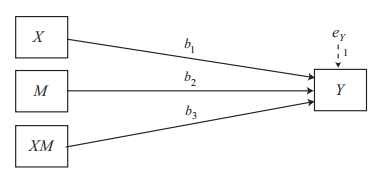
上述图片是调节的统计模型图，它转换成公式为：Y=b1X+b2M+b3XM+e=(b1+b3M)X+b2M+e

其中e是残差，b1-b3为分别对应的系数。

显而易见，X对Y的总影响其实是包括了两个部分，分别为b1+b3M，对吧。

当b3＝0时，M无论取什么值，X对Y的影响都是b1，斜率不变，此时不存在调节效应；
当b3≠0时，每当M取值增加1个单位，X对Y的影响也会增加b3个单位，X对Y的影响会受M的取值变化，斜率改变，此时调节效应才会存在。

所以b3就是调节效应量，能衡量调节效应的大小。

我们检验调节效应是否存在也就是判断b3是否=0。

【概念说明-显著性】

判断b3是否为0，其实就是看b3是否显著。

萜妹相信，显著不显著这个说法，小可爱们看到这里，肯定都听过。但是确实也会有些小可爱，明白显著是概率要小于0.05，但是不明白为什么要这样看。所以这里萜妹就单独用白话解释一下（完全是萜妹个人理解，如有疑惑，可以留言沟通）。

通常，抛硬币掷到字面的概率是0.5；掷骰子，掷到5或6的几率是0.33，这些都是随机几率。

可是，如果我连抛硬币5次，每次都是字面（0.5的5次方=0.03125），连掷3次骰子每次都是5或6，那这还是随机发生的吗？它大概率不是随机，而是受到某些因素影响了，对吧。

大家公认，当一件事情随机发生的几率小于0.05，但是它还是发生了时，我们就认为这不是随机的（至于为什么临界值是0.05，这是约定俗成的，萜妹也给不出解释）。

那么当一个系数的概率小于0.05，我们通常就说它显著。但这其实是个病句，显著怎么样？这在我们日常表达中被省略了，实际上应该是说它，显著不为0。

所以回到这个部分最开头。我们判断b3是否为0，可以看b3是否显著，也就是看b3这个系数的概率是否小于0.05。

【操作原理-建立交互项】

在数理上说完，如何衡量调节效应后，我们接下来介绍一下操作上检验调节效应有哪些需要准备的。

除了个别直接判断斜率是否改变的数据分析方式外，大部分的检验方式都需要建立交互项。

而建立交互项，又会涉及到另一个，大家常听，但不一定知道作用的操作——中心化/标准化。

将自变量和调节变量中心化/标准化后，计算二者的乘积，就可以得到交互项。

【概念说明-中心化/标准化】

首先说明这两个概念的定义：

中心化：变量减去均值，可得到均值为0的数据；
标准化：变量减去均值后，再除以标准差，可得均值为0、标准差为1的服从正态分布的数据。

二者的差别还是很显而易见的。做交互项的时候，起码要中心化，至于标准化则并非必须。

接下来说说为什么要进行这样的操作。以下观点来源于方杰和温忠麟等人的《基于多元回归的调节效应分析》，如有疑问可下载原文查看。

通俗的说，不进行中心化，那么X和XM以及M和XM间可能会产生多重共线性的问题，这虽然不会影响b3，但会影响b1和b2。

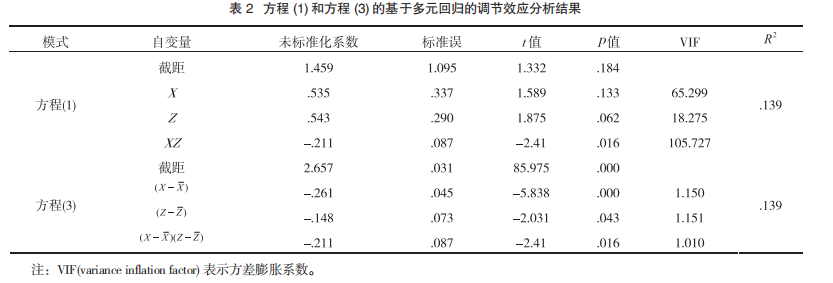
来源：参考文献[1]

另外就是不中心化的话，X、M取值为0时，不具备现实含义，不利于理解b1和b2的统计意义（不过写文章的时候，感觉很少去深究统计意义）。

关于这个方面的知识，萜妹只能算略知皮毛，中心化和标准化的作用、使用时机等感觉还是非常有学问的，萜妹也没把它吃的非常透，所以只能讲成这样啦。如果小可爱们实在理解不了，就还是记住这个结论好了~

【简单斜率检验】

计算出调节效应存在后，我们通常还有一个步骤是简单斜率检验。

理论上来说需要在M的不同取值水平下分别做回归分析以检验所谓的“X在M不同水平下的简单斜率”是否显著。但是，由于M是一个连续变量，不可能在所有取值下都做，所以通常我们选的三个特殊点分别为：均值以及均值加减一个标准差，这就是选点法的检验原理。

虽然选点法，存在一定的缺陷，但是目前的文章中，大多数还是沿用这种方法，所以暂时还是可以被接受的。

中介效应

【模型】

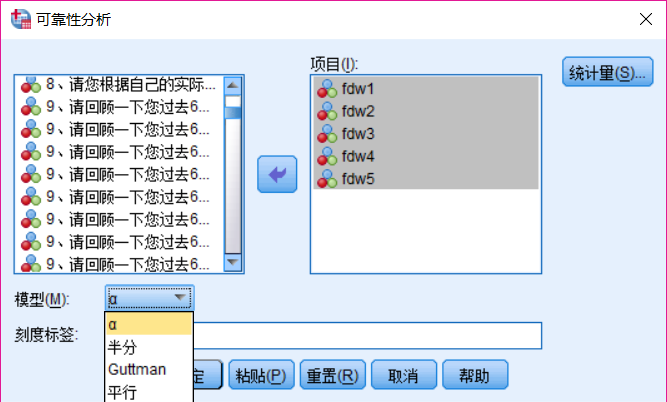
注：X是自变量，Y是结果变量，M是中介变量

【定义】

官方定义：考虑自变量X对因变量Y的影响，如果X通过影响变量M来影响Y，则称M。

萜妹理解：上面的解释挺清楚啦，萜妹就举些例子吧（以下例子基于常识，萜妹未进行科学考证，重点是帮助理解什么是中介，实际情况不一定对！！！）。

喝牛奶(X)是因为补充营养(M)，才有利于长高(Y)。
工资高(X)，可以买喜欢的东西(M)，所以更容易幸福(Y)。

【数理解释】

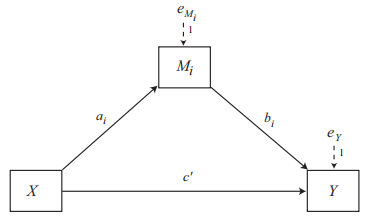
上述图片是中介的统计模型图，它转换成公式为：

M=aX+e1

Y=c’X+bM+e2

=c’X+b*(aX+e1)+e2

=(c'+ab)X+be1+e2

其中e1是M的残差，e2是Y的残差，a、b、c’为分别对应的系数。

显而易见，X对Y的总影响其实是包括了两个部分，分别为c’和ab。

c’被视为直接效应量，即X直接作用于Y的效应；
ab则被视为间接效应量，又是中介效应量，代表X通过M作用于Y的效应量。

所以要证明X会通过M作用于Y，需要证明ab显著不为0。

【概念说明-部分中介/完全中介】

中介部分，需要额外介绍的是部分中介与完全中介的差别。

从数理上来说，二者差别就是c’是否显著。显著则是部分中介，不显著则是完全中介。

完全中介的意思就是，X对Y的影响完全是通过M在起作用的；部分中介则是X既可以通过M起作用，也可以通过自身。拿上面的例子接着说明：

如果失去了营养价值(M)，喝牛奶(X)不能促进长高(Y)，那么这个时候，营养价值就是完全中介；
如果无法买喜欢的东西(M)，但是工资高(X)的人还是更容易幸福(Y)，那么买喜欢的东西就是部分中介。

啦啦啦，这篇推送就到这里啦。调节和中介其实是我们经常提到的东西，这篇推送的内容，萜妹总认为小可爱们都了解，所以每次介绍都是一笔带过。但是实际和学弟学妹接触过程中，萜妹发现这些概念有可能有的小可爱一知半解，导致后面的操作也只是知道要怎么做，而没办法理解。于是，这次就在具体操作前，跟大家细细的说一遍，希望看完的小可爱们，能理解调节和中介了啊~

至于具体的操作，因为萜妹已经写过很多次了，所以这次还是想和之前的推送有所差别。接下来的三周更新内容，大概包括①介绍什么是有中介的调节和有调节的中介；②具体操作的视频教程；③复杂模型（比如跨层模型、多中介、多调节模型）的简单介绍（尽量都给出优质的论文模板）。有兴趣的小可爱们就慢慢期待吧~

另外，如果有小可爱想提供复杂模型也欢迎留言告诉萜妹啦~

小可爱们，我们下周见吧~

参考文献：

[1]方杰, 温忠麟, 梁东梅,等. 基于多元回归的调节效应分析[J]. 心理科学, 2015(03):205-210.

往期推送

原文链接：