假设分析丨跨层模型
最常用的模型与原理都介绍完了,之前的内容大概率可以应付毕业的需求。不过有的小可爱们可能会继续做研究,或者是导师给的模型比较难,所以萜妹还会再更新部分有难度的模型,比如跨层模型。
现实背景
跨层模型其实是个发展的趋势,就近原则的取样方式会导致样本的质量有限,能联系公司或团队填写肯定对质量更有保障。
但是嵌套于团队的数据并非完全独立,他们会受一些共同因素影响。下面是一些小例子~
- 员工幸福感除了受个人因素影响外, 也跟领导的风格有关,真诚待人的领导和霸道、专制的领导肯定不一样。
- 学生成绩除了跟自身努力程度有关,还可能受到每个学校教学水平不同的影响。
另外,日记法最终也是采用跨层的逻辑在进行数据处理。此时,个体变成了level2的变量,而每天汇报的数据变成了level1的。
- 体重变化与每天的运动量、食物摄取量有关,但是这也受个人体质影响。比如有的人喝水都胖,但也有人狂吃不胖(好气啊!)
不跨层的弊端
如果我们不将其识别成跨层模型,那么有可能会得到错误的结论。萜妹就以体重为例。
假设现在有5个人,记录他们两天的食物热量与体重情况,如下表所示:
| 姓名 | 食物热量 | 体重 | 食物热量 | 体重 |
|---|---|---|---|---|
| A | 2100 | 101 | 2500 | 103 |
| B | 1900 | 102 | 2300 | 104 |
| C | 1700 | 103 | 2100 | 105 |
| D | 1500 | 104 | 1900 | 106 |
| E | 1300 | 105 | 1700 | 107 |
(注:热量单位为千卡,体重单位为斤。这个例子的数据并不科学,大家意会一下~)
这个时候,如果不分层,用这10个数据做回归,结果会变成这样:
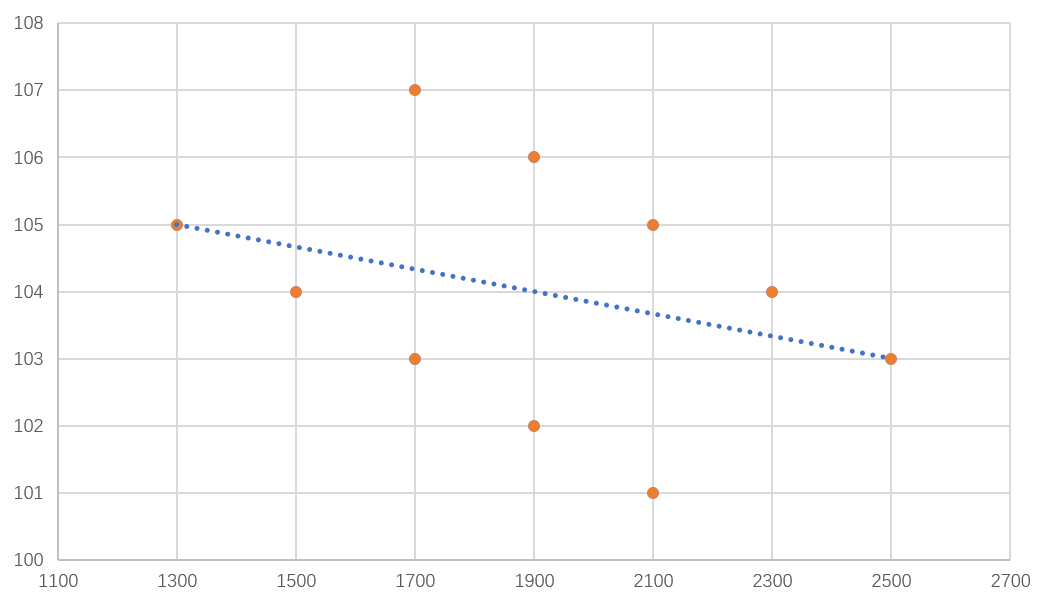
Y=-0.00166X+107.1667
这斜率竟然是个负的!那不是意味着吃的越多,反而能越轻(哪里会有这么好的事!),所以很明显,这不合理对吧。
那么,我们如果分组后再进行分析又会得到什么样的结果呢?
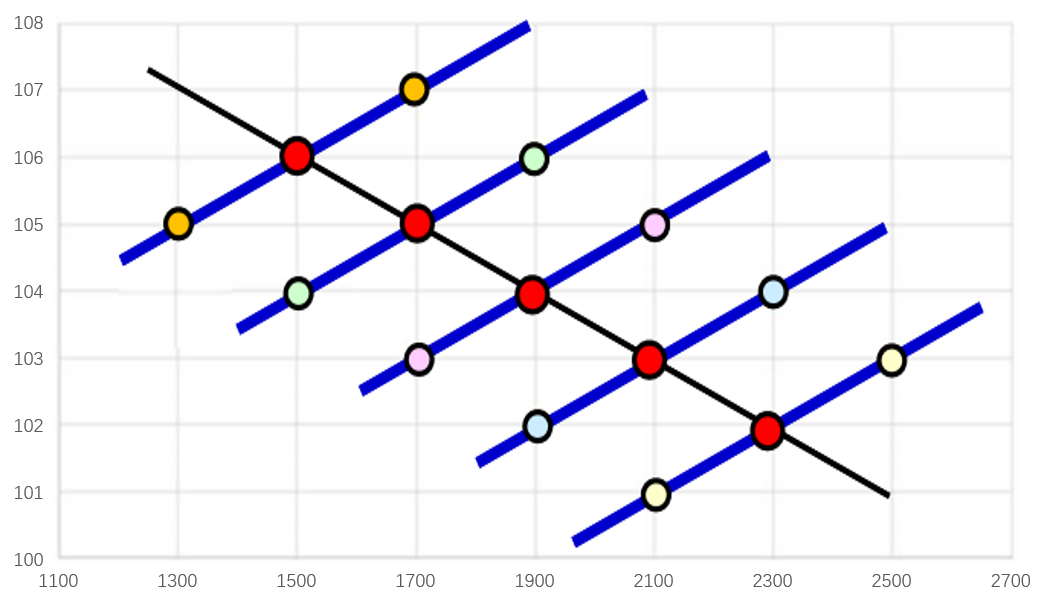
个体间(Level 2):Y=-0.005X+113.5
个体内(Level 1):Yj=0.005X+bj
上述的截距各不相同,因为每个人的特质不同啊。
当然,这也是一种比较理想的状态。体质不同,大家吸收情况不一样,所以现实中的斜率也并不会完全相同。
跨层数据中每个组别的斜率和截距都是所特有的,他们遵循着回归分析的规律。**但是如果不加区分将所有的数据放一起进行回归分析,那组内的这些因素关系可能被掩埋,得出的结论也有可能是错误的。**所以,当数据具有嵌套关系时,我们有做跨层分析的必要!
常见模型
下面主要是列举一些常见跨层模型。
类型 I 被中介的调节
2-1-1 ★
2-2-1
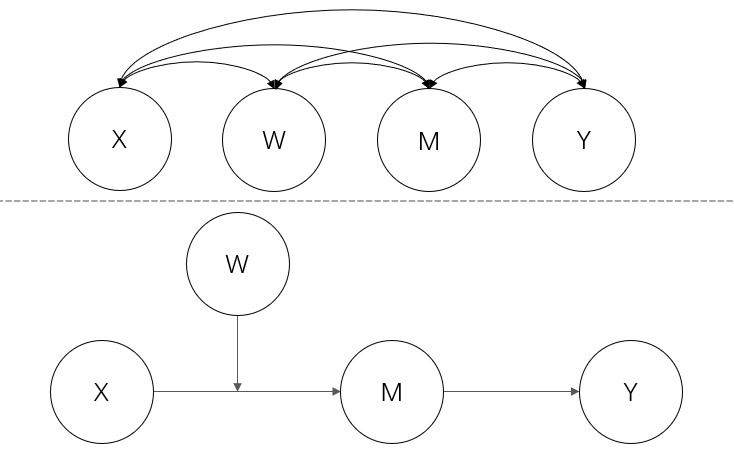
1-1-1
类型Ⅱ被中介的调节
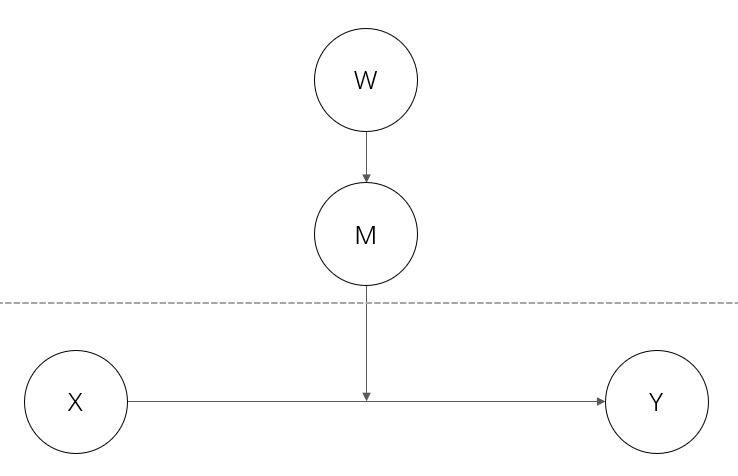
M 在 level 2 ★
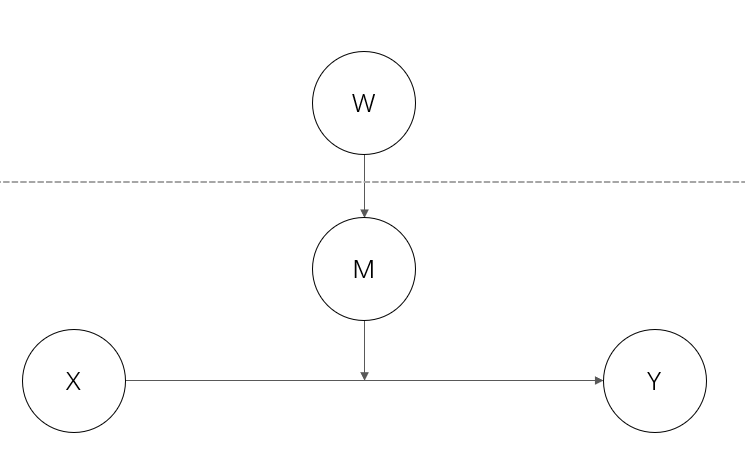
M 在 level 1
被调节的中介
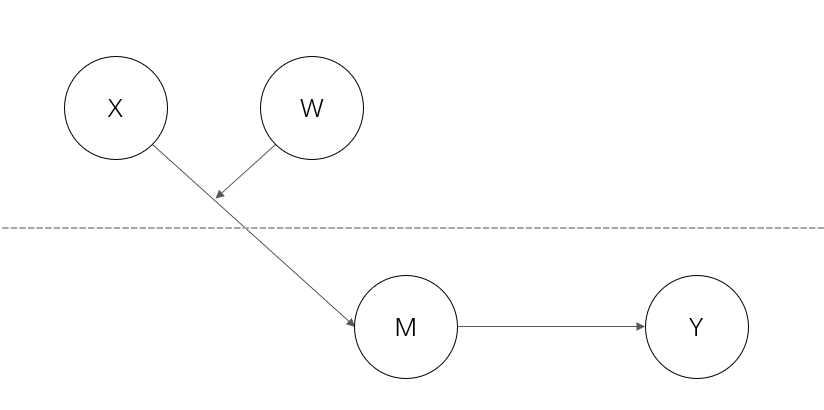
2-1-1
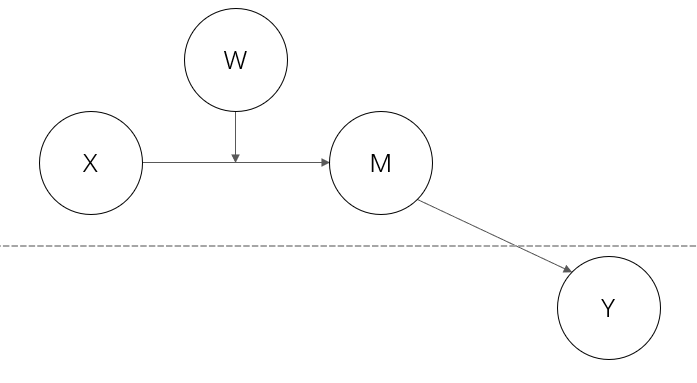
2-2-1
这两个模型,既可以被视为被中介的调节模型,也可以被视为被调节的中介模型。
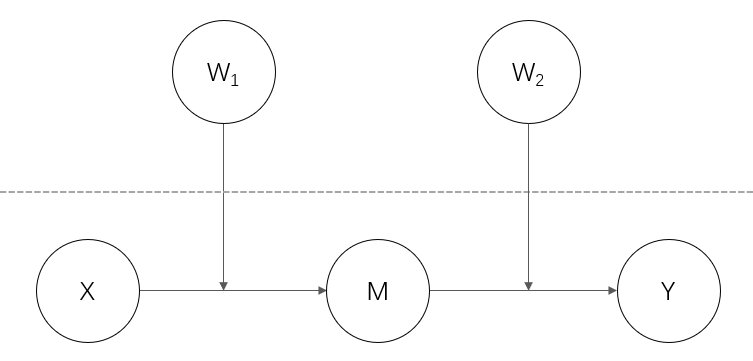
1-1-1 ★
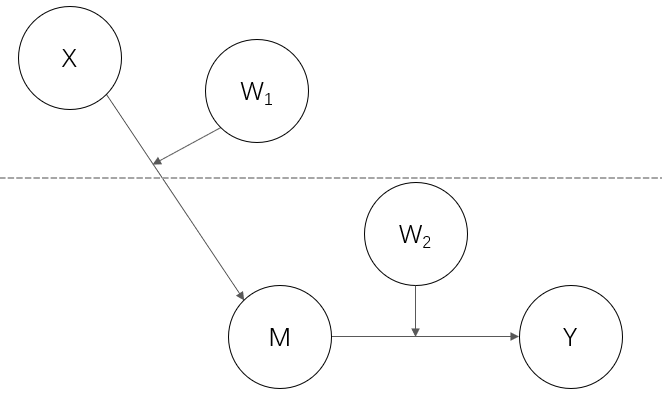
2-1-1
除了1-1-1以外,其他三个模型的中介效应仅存在于level 2。
以上标★的三个模型最为常见,萜妹以前详细介绍过它们的原理与语句,所以这里就不再展开说明。
有兴趣的小可爱可以在往期推送中回顾!
常见误区
误区1:变量可以自下而上进行调节
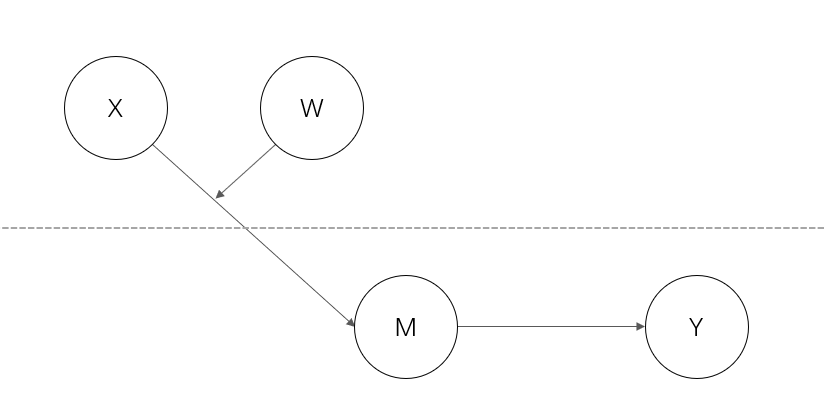
除了上述模型外,现实中还有其他的模型。但是有一些可能在数理上无法完美契合,比如下图这个。
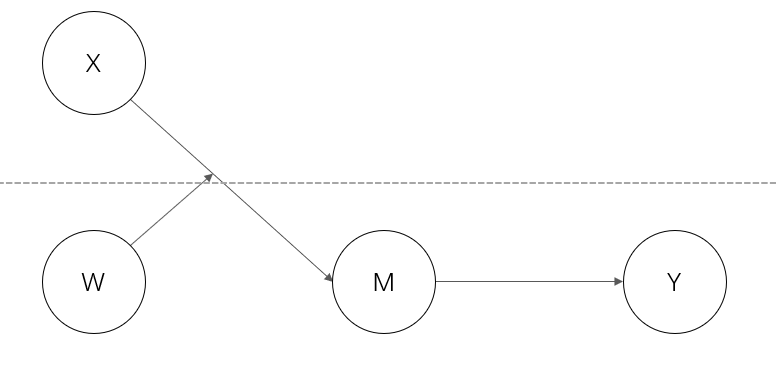
有一些已发表的文章,用的类似这样的模型,它在现实中确实也挺常见的。比如,不同特质的个体可能对领导风格有不同的反应。
但是,为什么萜妹还要单独说它,因为它其实是不符合数理逻辑的。原因如下:
首先,我们要明白,数理上 X 是不能影响 M 的,X 能影响的只有 M 的均值!
我们假设,X是学校的教学水平,M是学生成绩。
这是不是听起来还挺合理的,教学水平确实会影响学生成绩,好像能解释的通。但是,我们仔细思考一下:同一个学校的同学,他们成绩完全一样吗?大概率是不一样的对吧。
| 学校 | 学生 | 教学水平 | 学生成绩 |
|---|---|---|---|
| A | A1 | 60 | 480 |
| A | A2 | 60 | 520 |
| A | A3 | 60 | 440 |
| B | B1 | 80 | 600 |
| B | B2 | 80 | 580 |
此时,一个X对应了多个M,并且M不完全是因为随机误差而导致的不同,那么还能说 X 和 M 之间存在着因果关系吗?
所以,X 对 M 的影响其实是在level 2 发生的,教学水平能实际影响的是学生的平均成绩。平均成绩虽然来源于每个学生的成绩,但是二者是不同的。
那弄清楚 X 对 M 的作用方式后,又有一个新的问题:level 1 的 W 是怎么影响 level 2 的关系的?
代入例子中:学校教学水平与学校平均成绩的关系,会受到某个学生学习动机的影响吗?
| 学校 | 学生 | 教学水平 | 学生成绩 | 平均成绩 | 学习动机 |
|---|---|---|---|---|---|
| A | A1 | 60 | 480 | 480 | 70 |
| A | A2 | 60 | 520 | 480 | 90 |
| A | A3 | 60 | 440 | 480 | 70 |
| B | B1 | 80 | 600 | 590 | 90 |
| B | B2 | 80 | 580 | 590 | 85 |
如果学习动机可以影响的话,那为什么不同的 W 却会对应相同的 X 和 M,即对于学校A,主效应是已经确定了的,但是 A1 与 A2 调节变量的取值又是不一样的。这说明不同的 W 无法导致 X 与 M 的关系变化,与调节效应的原理相悖。
所以,调节变量是不可以自下而上进行调节的!
上述模型在实际处理过程中,还没有完全符合数理逻辑的解决方法。如果实在想用这种模型,可以考虑:①将所有变量放在level 1;②将所有变量放在 level 2。
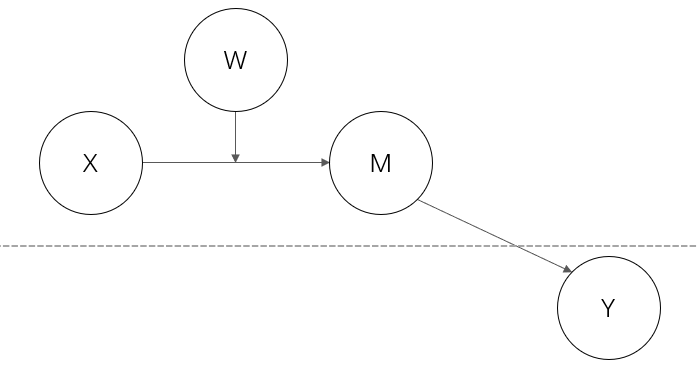
误区2:被中介的调节模型中自变量和调节变量可以位于不同层次
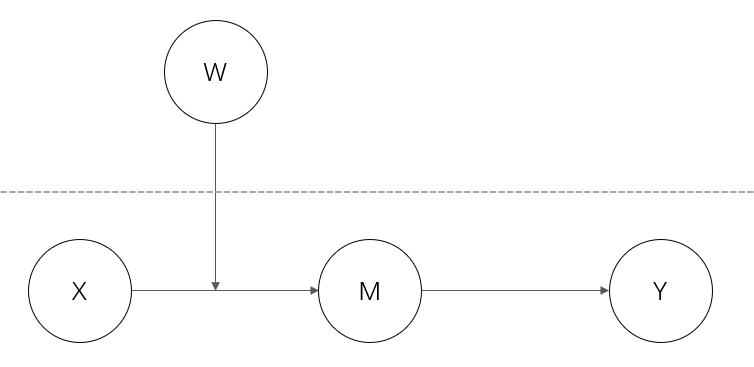
上图模型是不可以被视为被中介的调节模型的!
在类型 I 的被中介的调节模型中,需检验XW的系数,那么,X 与 W 应该具有系统对称性,即双方相互影响。
但实际上,X并不能影响 W 与 M 的关系,而 X 与 M 的关系却会随着 W 的取值而变化,这其实是被调节的中介模型的检验逻辑。
所以该模型只能是前半段被调节的中介模型,而无法成为被中介的调节模型。
啦啦啦,这篇推送就到这里啦。想把跨层单独拿出来写,第一是因为目前的趋势,单层有时候会被质疑;第二是因为它重要,一般培训都会单独介绍它;第三是,前阵子萜妹了解到SPSS也有了跨层分析的插件Mlmed,而且据说跟process一样比较好上手,所以想着掌握后给小可爱们介绍一下。
虽然目前,萜妹使用那个插件还在不停报错,但是我应该能在一周内研究出来……吧。当然,如果有已经掌握的小可爱,跟我沟通救救我更好!
那小可爱们,我们下周见吧~
往期推送
原文链接:
