R丨跨层效应的Monte Carlo估计
萜妹最近做了一次方法培训，正好趁着这个机会梳理了一些重难点，速速来分享一二。
今天先分享如何用R进行跨层效应的Monte Carlo估计。
由于Mplus没办法进行跨层Bootstrap的检验，所以我们往往需要借助R进行Monte Carlo分析。
有相关大佬做了网站，帮助大家实现简单的跨层中介估计，但实际中我们的模型各有不同，所以想根据自己的模型调整语句，先要了解这些语句的意义。
网址：http://quantpsy.org/medmc/medmc.htm
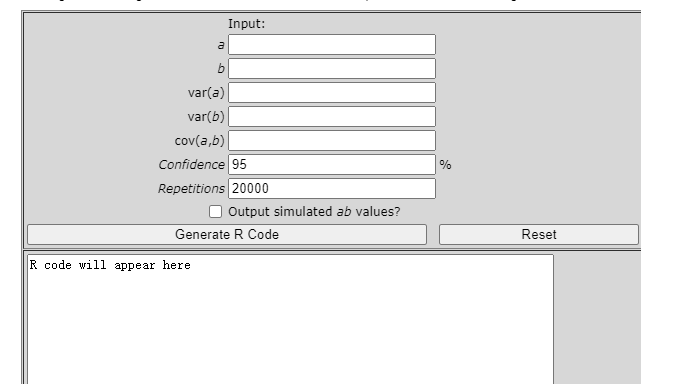原始界面
当我们填写相关数据，点击【Generate R Code】时，下方会生成相应语句。
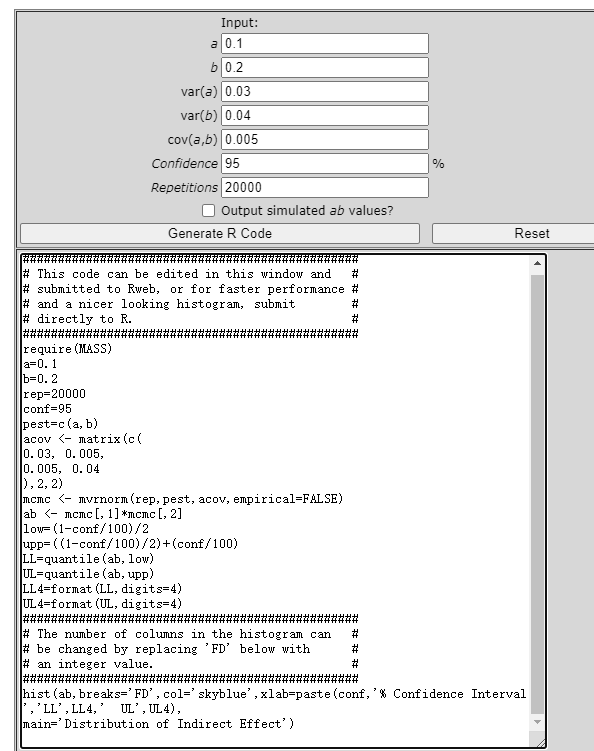网址自动生成R语句
我们把语句简单修改一下，可变成：
### 第一部分：数值输入
a=0.1
b=0.2
vara=0.03
varb=0.04
covab=0.005
### 第二部分：进行抽样
rep=20000
pest=c(a,b)
acov <- matrix(c(
vara, covab,
covab, varb
),2,2)
require(MASS)
mcmc <- mvrnorm(rep,pest,acov,empirical=FALSE)
### 第三部分：计算每个抽样的效应值
ab <- mcmc[,1]*mcmc[,2]
### 第四部分：生成置信区间
conf=95
low=(1-conf/100)/2
upp=((1-conf/100)/2)+(conf/100)
LL=quantile(ab,low)
UL=quantile(ab,upp)
LL4=format(LL,digits=4)
UL4=format(UL,digits=4)
### 第五部分：结果可视化
hist(ab,breaks='FD',col='skyblue',xlab=paste(conf,'% Confidence Interval ','LL',LL4,' UL',UL4),
main='Distribution of Indirect Effect')
第一个部分：数值输入
a=0.1 #计算效应量所涉及的系数1
b=0.2 #计算效应量所涉及的系数2
vara=0.03 #系数1的方差
varb=0.04 #系数2的方差
covab=0.005 #系数1与系数2的协方差
如何修改
在第一次写出完整R语句后，后续面对相同的模型可以仅修改此部分数值，即可直接运行获得结果。
如果模型修改涉及更多系数，则需要补充新的系数、系数的方差、和其他系数的协方差等所需内容。如涉及三个系数的被调节的中介检验：
a0=0.034 #计算效应量所涉及的系数1
b=0.176 #计算效应量所涉及的系数2
a1=0.072 #计算效应量所涉及的系数3
vara0=0.00837772 #系数1的方差
varb=0.00734839 #系数2的方差
vara1=0.00129167 #系数3的方差
cova0b=-0.00129363 #系数1与系数2的协方差
cova0a1=0.00169509 #系数1与系数3的协方差
cova1b=-0.000502121 #系数2与系数3的协方差
w0=0.7578 #调节变量标准差
第二部分：进行抽样
rep=20000 #抽样次数
pest=c(a,b) #一个给定均值的向量
acov <- matrix(c(
vara, covab,
covab, varb
),2,2) #定义协方差矩阵
require(MASS) #调用MASS包
mcmc <- mvrnorm(rep,pest,acov,empirical=FALSE) #将随机结果命名为mcmc
这个部分的语句是为了调用MASS包，通过mvrnorm()函数，从指定的多变量正态分布中产生多个样本，并命名为mcmc。
mvrnorm()函数介绍
mvrnorm(n = 1, mu, Sigma, tol = 1e-6, empirical = FALSE, EISPACK = FALSE)
- n：生成的样本数量；
- mu：指定向量的均值；
- Sigma: 指定向量的对称协方差矩阵；
- tol: （相对于最大方差）对Sigma缺乏正确定性(positive-definiteness)的容忍度；
- empirical: 如果为真，则mu和Sigma指定样本(empirical)而非总体(population)的均值和协方差矩阵。
- EISPACK：除FALSE以外的值是错误的。
对应到我们的公式里，其实是对一个协方差矩阵为acov的、给定均值的向量pest，重复抽样rep次，最终生成了一个名为mcmc的数组。
mcmc <- mvrnorm(rep,pest,acov,empirical=FALSE)
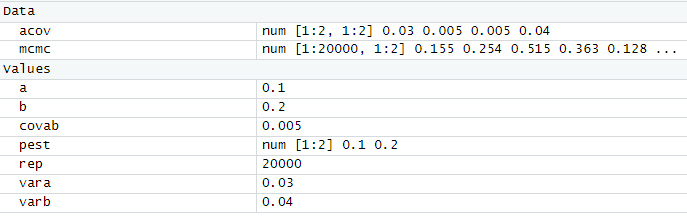
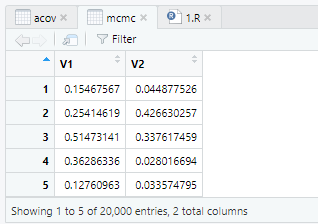
一个额外的提醒：
acov <- matrix(c(
vara, covab,
covab, varb
),2,2)
acov <- matrix(c(vara, covab,covab, varb),2,2)
上述两种表达都能生成矩阵。语句的本质逻辑是，根据输入的4个数字，生成2*2的矩阵。
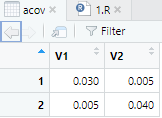
如何修改
如果我们的效应值只涉及两个系数，那此处可以不变。如果我们所检验的模型涉及更多系数，则需要对应添加。
有的调节效应值为 ，此处涉及、、三个系数，那么pest和acov也需要对应修改，如：
pest=c(a0,b,a1)
acov <- matrix(c(
vara0,cova0b,cova0a1,
cova0b,varb,cova1b,
cova0a1,cova1b,vara1
),3,3)
第三部分：计算每个抽样的效应值
计算我们所需的效应值，比如中介效应的。
ab <- mcmc[,1]*mcmc[,2]
这里的意思是，将mcmc的第一列数据与mcmc的第二列数据相乘。
因为pest=c(a,b)，所以第一列关于a，第二列关于b。
运行完会得到20000个效应值。
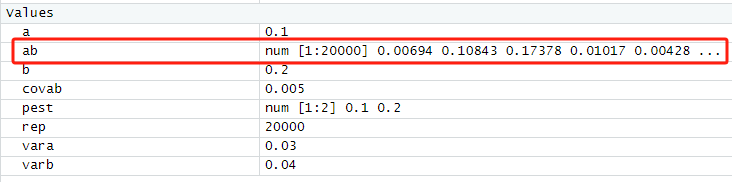
如何修改
调节效应效应值为，那我们可以对应修改为：
ah <- mcmc[,1]+w0*mcmc[,3]
al <- mcmc[,1]-w0*mcmc[,3]
abh <- ah*mcmc[,2]
abl <- al*mcmc[,2]
ind=abh-abl
第四部分：生成置信区间
conf=95 #置信区间范围
low=(1-conf/100)/2 #置信区间低值百分比为low
upp=((1-conf/100)/2)+(conf/100) #置信区间高值百分比为high
LL=quantile(ab,low)#计算排序后在区间底部的效应值为LL
UL=quantile(ab,upp)#计算排序后在区间底部的效应值为UL
LL4=format(LL,digits=4)#将LL保留四位有效数字输出为LL4
UL4=format(UL,digits=4)#将UL保留四位有效数字输出为UL4
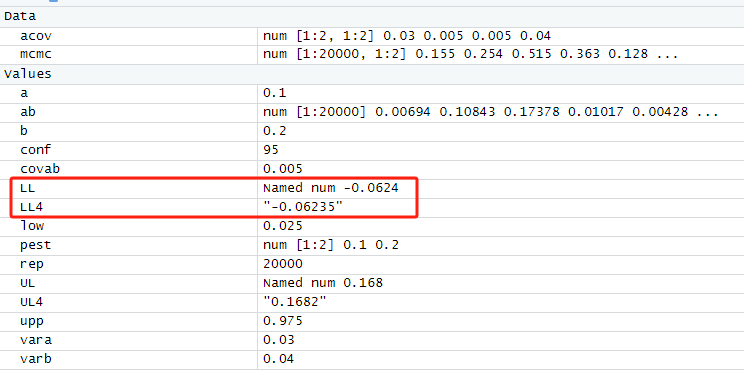
如何修改
如果模型改变，这个部分需要修改ab。
个人建议尽量把模型的效应值统一用ind表示，这样后续这些部分即使修改模型仍是估计ind，而不需要每次变来变去。
LL=quantile(ind,low)#计算排序后在区间底部的效应值为LL
UL=quantile(ind,upp)#计算排序后在区间底部的效应值为UL
第五部分：结果可视化
hist(ab,breaks='FD',col='skyblue',xlab=paste(conf,'% Confidence Interval ','LL',LL4,' UL',UL4),
main='Distribution of Indirect Effect')
这里的意思是根据ab的20000个数据，制作一个直方图，样式是’FD'，横坐标为“conf,'% Confidence Interval ‘,‘LL’,LL4,’ UL',UL4”，主标题为“Distribution of Indirect Effect”
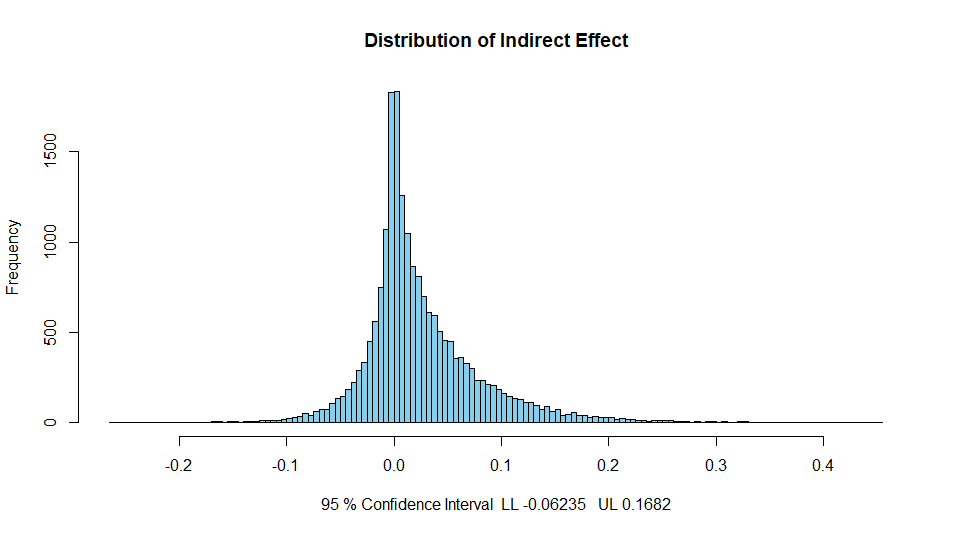
如何修改
同理，也需将ab修改为ind。
语法汇总
单因素前半段被调节的中介模型
require(MASS)
a0=0.034 #计算效应量所涉及的系数1
b=0.176 #计算效应量所涉及的系数2
a1=0.072 #计算效应量所涉及的系数3
vara0=0.00837772 #系数1的方差
varb=0.00734839 #系数2的方差
vara1=0.00129167 #系数3的方差
cova0b=-0.00129363 #系数1与系数2的协方差
cova0a1=0.00169509 #系数1与系数3的协方差
cova1b=-0.000502121 #系数2与系数3的协方差
w0=0.7578 #调节变量标准差
rep=20000
pest=c(a0,b,a1)
acov <- matrix(c(
vara0,cova0b,cova0a1,
cova0b,varb,cova1b,
cova0a1,cova1b,vara1
),3,3)
mcmc <- mvrnorm(rep,pest,acov,empirical=FALSE)
ah <- mcmc[,1]+w0*mcmc[,3]
al <- mcmc[,1]-w0*mcmc[,3]
abh <- ah*mcmc[,2]
abl <- al*mcmc[,2]
ind=abh-abl
conf=95
low=(1-conf/100)/2
upp=((1-conf/100)/2)+(conf/100)
LL=quantile(ind,low)
UL=quantile(ind,upp)
LL4=format(LL,digits=4)
UL4=format(UL,digits=4)
hist(ind,breaks='FD',col='skyblue',xlab=paste(conf,'% Confidence Interval ','LL',LL4,' UL',UL4),
main='Distribution of Indirect Effect')
单因素后半段被调节的中介模型
require(MASS)
b0=0.034 #计算效应量所涉及的系数1
a=0.176 #计算效应量所涉及的系数2
b1=0.072 #计算效应量所涉及的系数3
var1=0.00837772 #系数1的方差
var2=0.00734839 #系数2的方差
var3=0.00129167 #系数3的方差
cov12=-0.00129363 #系数1与系数2的协方差
cov13=0.00169509 #系数1与系数3的协方差
cov23=-0.000502121 #系数2与系数3的协方差
w0=0.7578 #调节变量标准差
rep=20000
pest=c(b0,a,b1)
acov <- matrix(c(
var1,cov12,cov13,
cov12,var2,cov23,
cov13,cov23,vara3
),3,3)
mcmc <- mvrnorm(rep,pest,acov,empirical=FALSE)
bh <- mcmc[,1]+w0*mcmc[,3]
bl <- mcmc[,1]-w0*mcmc[,3]
abh <- ah*mcmc[,2]
abl <- al*mcmc[,2]
ind=abh-abl
conf=95
low=(1-conf/100)/2
upp=((1-conf/100)/2)+(conf/100)
LL=quantile(ind,low)
UL=quantile(ind,upp)
LL4=format(LL,digits=4)
UL4=format(UL,digits=4)
hist(ind,breaks='FD',col='skyblue',xlab=paste(conf,'% Confidence Interval ','LL',LL4,' UL',UL4),
main='Distribution of Indirect Effect')
这次的推送就到这里啦，希望对小可爱们有所帮助吖！其他的模型也可以根据上述原理进行对应修改，小可爱们可以多多探索哦。