最近后台有好些小可爱询问QCA的问题，所以萜妹决定更新一篇相关主题的内容。

各部分语法介绍

Step 0：安装并加载R包

如果第一次使用R包，需要先安装。

install.packages("QCA")

但在每次使用时都需要重新加载R包。

library(QCA)

Step 1：导入原始数据

首先，QCA包里自带了一些数据，方便我们后续演练，可直接调用。

data(LR)

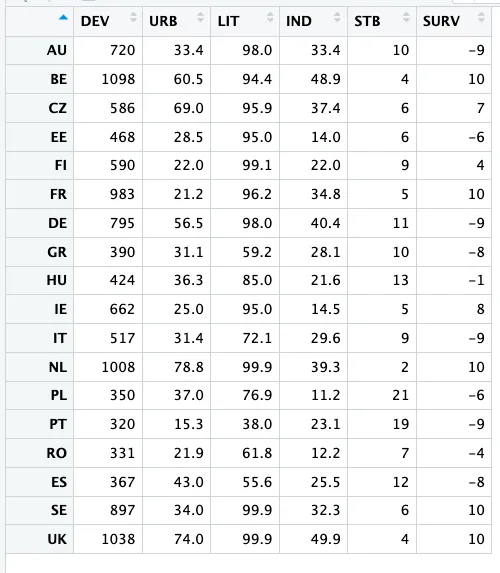图片LR数据结构

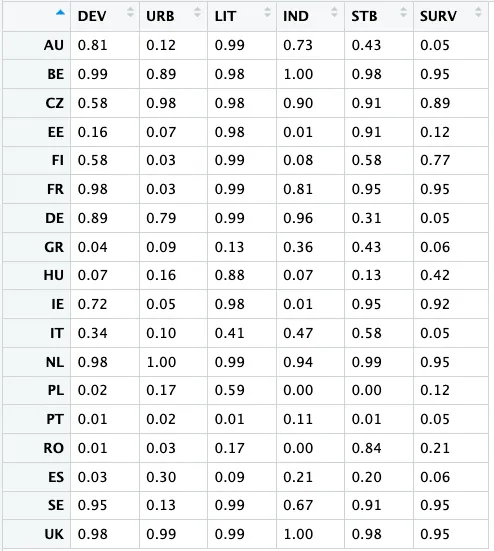图片LF数据结构

萜妹后续的演示以上述数据为例。

当然我们也可以自己导入数据，导入方法很多，这里仅介绍几种，掌握一种就行。

语句版

library(readr)
LF <- read_csv("data/Study 1 Data.csv")

所用R包：readr。

  • 第一行：调用readr包。
  • 第二行：将【data/Study 1 Data.csv】读取，并命名为【data】。

运行后可以在Environment里看到data。

图片img

点击版

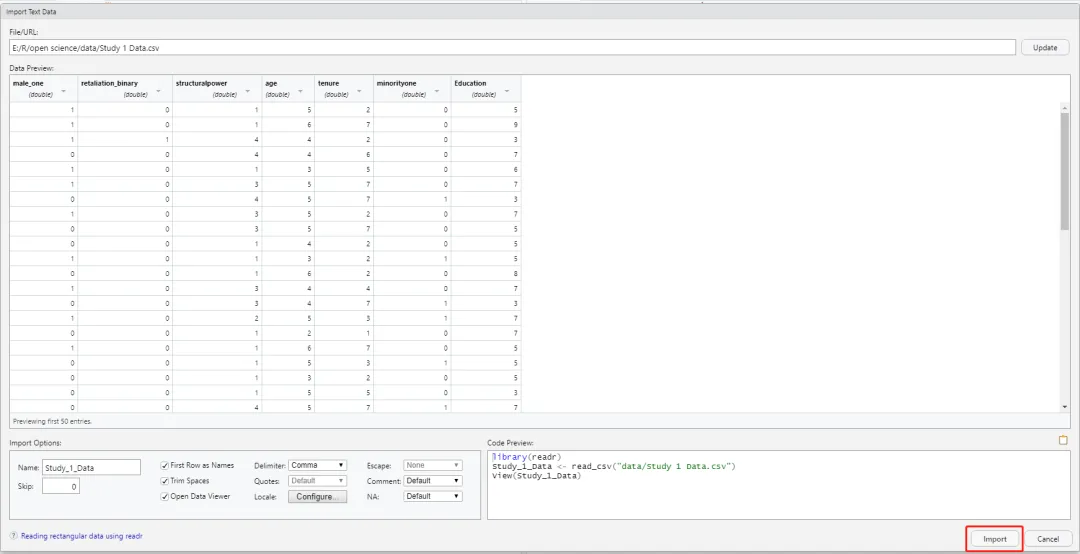
如果不想写语法，大家还可以在RStudio里找到文件点击Import Dataset。

图片img

点击Import。

图片img

不过这样导入的数据名是原始的，所以我们可以在import options里进行修改。

Step 2：校准

选择校准点

如果是想校准成清晰集，或者多值集，我们可以利用findTh语法来寻找校准点。

findTh(x, n = 1, hclustm = "complete", distm = "euclidean", ...)
  • X：对象
  • N：阈值数量，默认为1。
  • ……

图片

模糊集的校准点选择可以参考模糊集校准心得、QCA操作参考文献，这里就不再赘述。

数据校准

校准过程推荐使用calibrate函数。

#清晰集
LR$a1 <- calibrate(LR$DEV,type="crisp",thresholds=550)
#多值集
LR$a2 <- calibrate(LR$DEV,type="crisp",thresholds="550,850")
#模糊集
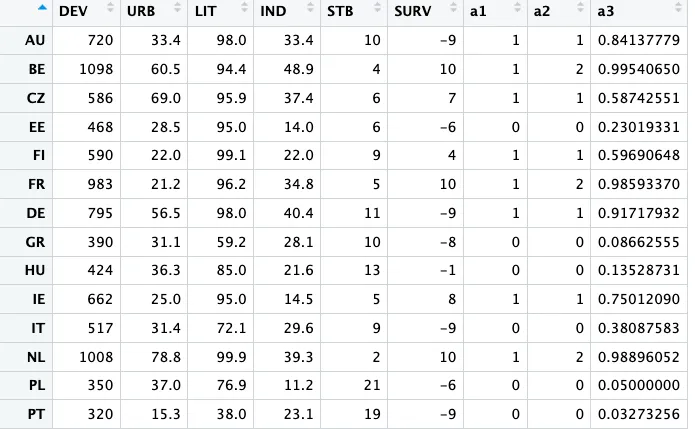
LR$a3 <- calibrate(LR$DEV,thresholds="e=350,c=550,i=850")
  • type默认为模糊集校准；
  • e代表完全不隶属；c代表交叉点；i代表完全隶属。

图片

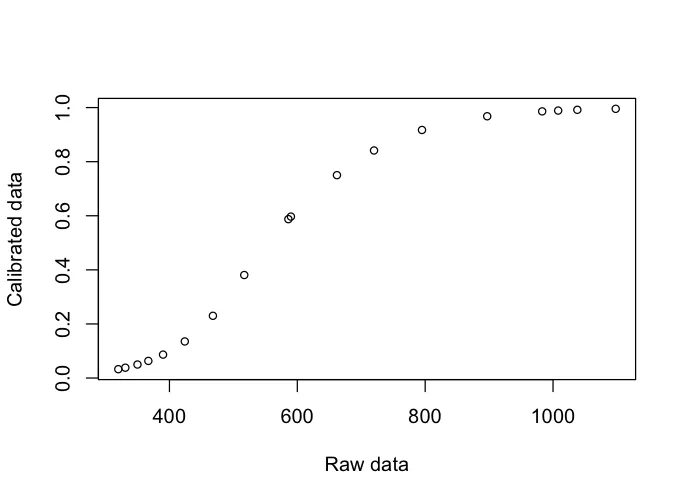
我们可以做图看到原始数据与校准数据的关系。

plot(LR$DEV, LR$a3,xlab="Raw data",ylab="Calibrated data",cex =0.8)

图片

Step 3：必要性分析

查看单因素必要性

pof("DEV<=SURV",data=LF)
  • 【DEV】为条件；
  • 【SURV】为结果；
  • 【LF】为校准后的数据。

图片

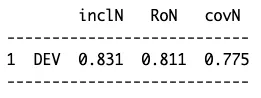
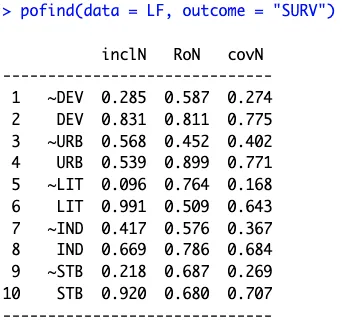
  • inclN为一致性；
  • RoN为相关性或可译为切题性；
  • covN为原始覆盖度。

也可以利用简化版的pofind函数，一次性计算所有条件的必要性。

pofind(data = LF, outcome = "SURV")

图片

绘制XY plot

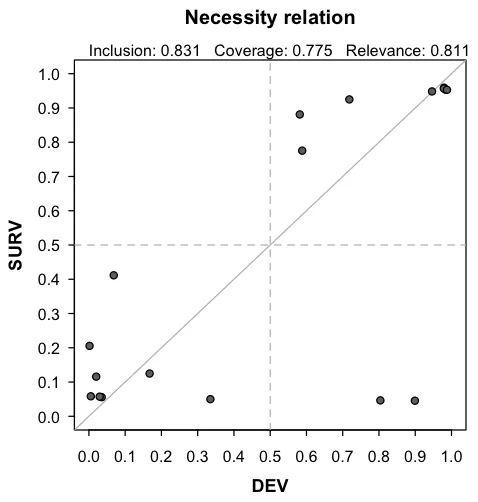
如果想画图可利用XYplot函数实现。

XYplot(DEV,SURV,data=LF,jitter = TRUE,relation="necessity")

图片

探索所有必要条件

有时候必要条件并不是由单因素独立作用的，我们可以利用superSubset函数，探索出多因素必要条件。

superSubset(LF,outcome = "SURV",incl.cut = 0.9, ron.cut = 0.6)
  • incl.cut意为一致性最低为0.9，低于此值舍弃；
  • ron.cut意为切题性最低为0.6。

图片

这些信息在后续布尔运算最小化时可能会派上用场。

Step 4：充分性分析

真值表构建

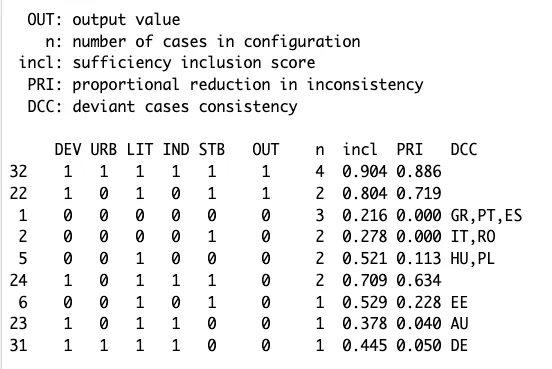
ttLF<-truthTable(LF,outcome = "SURV",incl.cut=0.8,show.cases = TRUE,dcc=TRUE, sort.by = "OUT,n")
ttLF
  • show.cases意为显示案例；
  • dcc只在show.cases被激活时出现，意为一致性异常的案例，它会显示真实的逻辑余项，即在组态中隶属分数大于0.5，但在结果中隶属分数小于0.5。
  • sort.by = “OUT,n"意为按OUT的结果排序。

图片

布尔最小化

各种解的得出均利用minimize函数，只是输入语句略有差异。

各种解的差异在于对逻辑余项的处理方式。通俗来说，复杂解拒绝所有逻辑余项，简单解接受所有逻辑余项，中间解则看情况取舍。详见定性比较分析之进阶篇。

复杂解

consLF <-minimize(ttLF,details = TRUE)
consLF

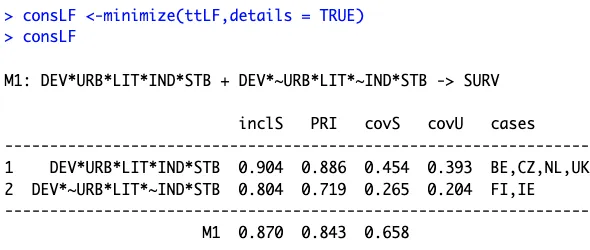图片复杂解

简约解

pLF<-minimize(ttLF,include = "?",details = TRUE)
pLF

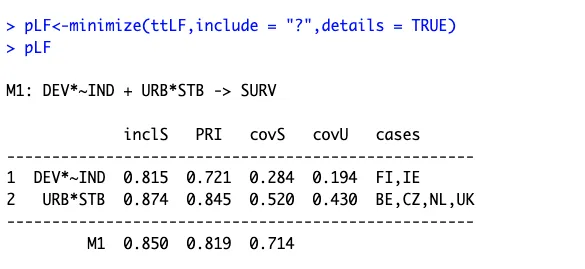图片简约解

中间解 有三个函数涉及对逻辑余项的处理，include、exclude和dir.exp。

  • include说明在最小化中包含什么；
  • exclude说明在最小化中排除什么；
  • dir.exp制定方向期望，例如假设所有条件均导致结果存在，则dir.exp指定向量均为1；若不指定方向，则为-。

首先，利用findRows函数，确定相互矛盾的简化假设，方便后续排除。

SA1<-findRows("~LIT+~STB+~DEV*~URB*~IND",ttLF)
SA2<-findRows(obj=ttLF,type = 2)
SA3<-findRows(obj=ttLF,type = 3)
  • type(1)为默认，排除了与必要性分析不符合的结果；
  • type(2)排除了结果存在与结果不存在二个集合中相互矛盾的简化假设；
  • type(3)排除了结果存在与结果不存在二个集合中同时子集关系。
iLF<-minimize(ttLF,include = "?",dir.exp="1,1,1,1,1",details = TRUE,show.cases = TRUE)
iLF

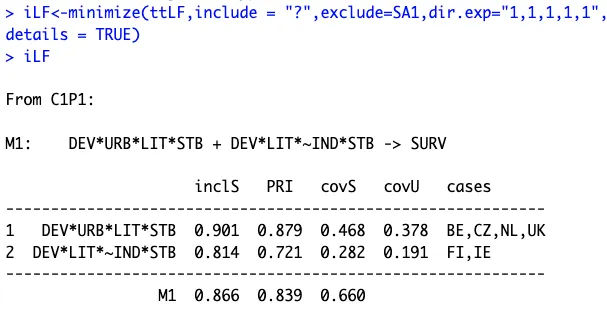图片中间解

整体语法汇总

# Step 0：安装并加载R包
install.packages("QCA")
library(QCA)
# Step 1：导入原始数据
library(readr)
LF <- read_csv("data/Study 1 Data.csv")
# Step 2：校准
##清晰集
LR$a1 <- calibrate(LR$DEV,type="crisp",thresholds=550)
##多值集
LR$a2 <- calibrate(LR$DEV,type="crisp",thresholds="550,850")
##模糊集
LR$a3 <- calibrate(LR$DEV,thresholds="e=350,c=550,i=850")
##Plot
plot(LR$DEV, LR$a3,xlab="Raw data",ylab="Calibrated data",cex =0.8)
# Step 3：必要性分析
pof("DEV<=SURV",data=LF)
pofind(data = LF, outcome = "SURV")
superSubset(LF,outcome = "SURV",incl.cut = 0.9, ron.cut = 0.6)
## XYPlot
XYplot(DEV,SURV,data=LF,jitter = TRUE,relation="necessity")
# Step 4：充分性分析
## 真值表构建
ttLF<-truthTable(LF,outcome = "SURV",incl.cut=0.8,show.cases = TRUE,dcc=TRUE, sort.by = "OUT,n")
ttLF
##布尔最小化
### 复杂解
consLF <-minimize(ttLF,details = TRUE)
consLF
### 简约解
pLF<-minimize(ttLF,include = "?",details = TRUE)
pLF
### 中间解
SA1<-findRows("~LIT+~STB+~DEV*~URB*~IND",ttLF)
SA2<-findRows(obj=ttLF,type = 2)
SA3<-findRows(obj=ttLF,type = 3)
iLF<-minimize(ttLF,include = "?",dir.exp="1,1,1,1,1",details = TRUE,show.cases = TRUE)
iLF

这篇推送就到这里啦，希望对大家有所帮助。

相关资料参考：

图片

往期推送

原文链接