RSA丨多项式回归之基本模板
Cole, M. S. , Carter, M. Z. , & Zhang, Z. . (2013). Leader-team congruence in power distance values and team effectiveness: the mediating role of procedural justice climate. Journal of Applied Psychology, 98(6), 962-973.
前几天有朋友问我,QCA遇到类变量的时候怎么办,有没有文章可以参考。
在把文章发过去后,我突然想到,我要不开个新模块专门介绍各种方法的优质模板吧。
之前一直没做过文献方面的输出,因为萜妹在这方面比操作要弱些,但想要更进一步,文献阅读也必不可少。所以让我边复习、边分享、边学习地开启这个新模块吧~
原文链接:
整体介绍
摘要
本文考察了领导者与团队之间权力距离一致性对团队有效性的影响。本文假设这些价值观间的一致性会不同程度的预测团队有效性,而程序正义氛围起中介作用。利用多源数据和多项式回归,本文发现领导者和团队权力距离值的相似性(差异性)会对团队的公平氛围产生影响,并最终影响团队有效性(团队绩效和团队组织公民行为)。本文的结论是:为了充分理解权力距离的含义,学者应该考虑领导者和团队成员的多重视角。
We examine the effect of (in)congruence between leaders’ and teams’ power distance values on team effectiveness. We hypothesize that the (in)congruence between these values would differentially predict team effectiveness, with procedural justice climate serving as a mediator. Using multisource data and polynomial regression, we found that similarities (and differences) between leaders’ and their teams’ power distance values can have consequential effects on teams’ justice climate and, ultimately, their effectiveness (viz., team performance and team organizational citizenship behavior). We conclude that to fully understand the implications of power distance, one should consider the multiple perspectives of both leaders and team members.
理论模型
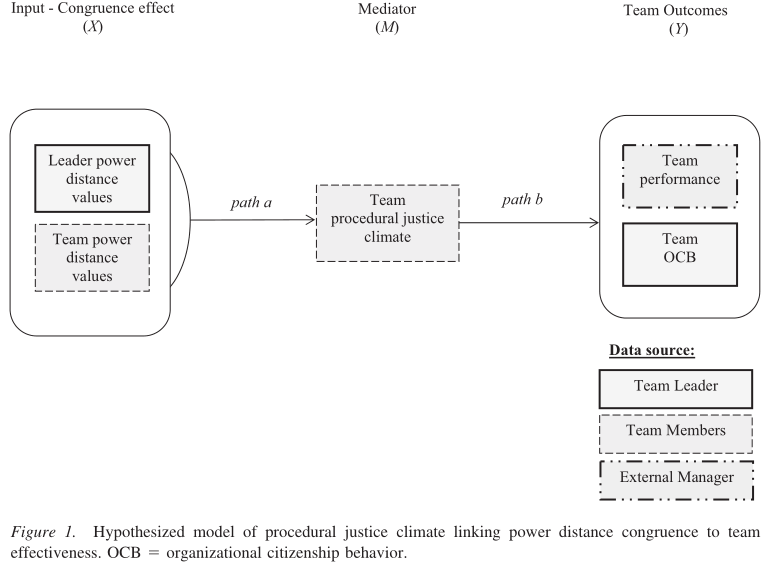
模型假设
PJC代表程序公平氛围,OCB代表组织公民行为。
- H1:领导-团队权力距离一致性与团队PJC正相关;
- H2:相比于领导权力距离低于团队权力距离时,领导权力距离高于团队权力距离时,PJC的下降更剧烈;
- H3:领导-团队权力距离一致性会通过PJC对(a)团队绩效和(b)团队OCB造成积极的间接影响。
研究方法
样本及程序
第一段描述了样本的选取,介绍了所选公司为何符合此次调研。
第二段描述了问卷收集的三个来源,分别是:团队成员、正式团队领导和外部高层管理人员(如团队之上的一个层级)。
如模型图所示,各变量与来源对应关系如下:
- 团队成员:汇报个人的权力距离、程序正义感知和人口统计学变量;
- 团队领导:汇报个人的权力距离和人口统计学变量,并对每一位团队成员的OCB进行评价;
- 外部领导:评估团队的整体表现。
第三段根据不同公司,分别描述了被试的具体应答情况。
For Company A, the average actual team size was five, ranging from three to six team members. Of the 52 teams in this company, we obtained usable data from 43 teams, yielding a team-level response rate of 83%. On average, three team members (SD=0.52) completed the survey (not including the formal team leader) for a mean within-team response rate of 74%. A representative team member was male (81%), 26 years of age, and with an average organizational tenure of 2.2 years. A representative team leader was male (77%), 31 years of age, and with an average organizational tenure of 5.4 years. For Company B, ……
第四段回答了无应答者偏差。
We pooled the teams (n=78) into one data set to increase the statistical power of our analyses.3We examined the potential for nonresponse bias based on personnel records. Across both companies, there were no significant differences between respondents and nonrespondents on gender, age, and organizational tenure.
测量
测量部分和其他文章没什么区别,萜妹这里仅附上对权力距离测量的描述,其他不做说明。
We assessed team leaders’ and team members’ power distance values using the six-item measure developed by Dorfman and Howell (1988). Leaders and team members provided a self-ascriptive rating of their personal values; that is, the items referred to individuals’ conceptions about how managers and subordinates should behave in general (not specific to any one organization or work unit). Sample items include “Managers should make most decisions without consulting subordinates” and “Subordinates should not disagree with managers’ decisions.” For leader power distance, the reliability was .89. For team power distance, we followed prior research (J. Yang et al., 2007) and used a direct consensus composition model (Chan, 1998) when assessing members’ responses. The reliability for team power distance was .94.
这里是团队层的研究,所以需要把个体层的权力距离先聚合到团队层。并且,领导和团队的内部一致性系数应分开报告。
数据聚合
因为是团队层研究,所以需要报告ICC、Rwg等相关指数。
Corresponding analysis of variance demonstrated that team power distance, F(77, 173) ? 2.19; PJC, F(77, 173) =3.89; and team OCB, F(77, 173) =2.83, differed significantly (p< .01) across teams. The intraclass correlation (ICC1) for these three variables were .27 for team power distance, .47 for PJC, and .36 for team OCB. The reliability of the team-level means, as reflected by ICC(2) estimates, was .54 for team power distance, .74 for PJC, and .65 for team OCB. In regard to within-team agreement (rwg[J]; James, Demaree, & Wolf, 1984), we computed a lower and an upper bound estimate of agreement by considering two null distributions in the rwg(J)equation (Biemann, Cole, & Voelpel, 2012). For the lower bound, we selected a slightly skewed distribution (σE2=2.9) given that a positive leniency of participant responses could be expected. The rectangular distribution (σE2=4.0) was used because it is known to yield an upper bound estimate. The mean rwg(J)scores suggested strong within-team agreement (Biemann et al., 2012, p. 73), with estimates of .79 and .86 for team power distance, .97 and .98 for PJC, and .97 and .99 for team OCB.
分析策略(★)
与常规的数据分析文章不同,多项式回归会在研究方法的最后部分额外介绍分析策略,即从数理角度说明假设成立需要哪些条件。
这篇文章的这个部分写的比较详细,为便于小可爱们后续参考,萜妹会把该部分完整翻译。蓝色字体为根据自身研究需要替换的内容。
(原文和公式不好手打,我就直接截图过来了)

**一致性效应的检验。**运用多项式回归和响应面方法(see Edwards, 2002; Edwards & Cable, 2009),我们通过估计以下方程来检验假设1和2(为了简化,我们省略了所有控制变量):
其中M代表中介变量(即PJC),L和T分别是领导和团队权力距离。然后,我们使用回归系数绘制三维响应面,其中L和T绘制在水平轴上,M绘制在垂直轴上(Edwards & Parry,1993)。


为了验证假设1,我们检验了绘制响应面的三个关键特征。首先,我们检查了响应面上的不一致线(L=–T)。为了支持假设的一致性效应,不一致线的曲率(b3–b4+b5)应为负值(向下弯曲)。其次,我们检查了响应面的第一主轴。如果该轴的斜率p11=1.0和截距p10=0,则响应曲面的脊沿一致线运行。这一发现为假设1提供了额外的支持,表明当领导-团队权力距离值相等时,PJC最大化。由于第二个条件涉及方程1回归系数的非线性组合,我们使用10000次的Bootstrap计算p11和p10的95%偏差校正置信区间(CIs)(Edwards, 2002; Edwards & Parry,1993)。第三,我们确定一致线(L=T)的曲面是否平坦 。如果表面沿着一致线是平坦的,表明无论对齐的领导-团队权力距离值是低还是高,PJC的水平是相同的,则其斜率(b1+b2)和曲率(b3+b4+b5)与零无显著差异。
根据Edwards和Cable(2009)的观点,即使不满足所有的条件也并不一定排除一致性效应。然而,第一个条件必须满足。此外,如果第一个和第二个条件得到了证实,但第三个条件被拒绝,我们假设的一致性效应在PJC的最大水平取决于领导者和团队权力距离的高低的情况下,仍然可以推断出假设成立。Edwards和Cable(2009)认为,第三个条件不那么重要,因为它评估的是“与理想表面的偏差”。根据Edwards和Cable(2009)的逻辑,我们虽检查第三种条件,但优先考虑前两种条件。这意味着如果第一和第二个条件得到满足,假设1则成立。
PS:这里萜妹再额外提一嘴。大多后续检验一致性的文章已经不会提第三个条件了;有些文章也并没有在分析策略中提出第二个条件。但我个人的数理理解是,第二个条件也是需要满足的。不然即使曲线出现最高点,但最高点与一致性线不重合,那么是无法说明二者一致时取值最高的。不过第二个条件的计算复杂一些,所以很多文章可能都没有计算。萜妹对于一致性检验的建议是:第一个条件一定要提出与检验;第二个条件可以在撰写时不提,但也尽量检验其满足;第三个条件可忽视。

为了检验假设2中的不对称不一致效应,我们计算了横向位移量([b2–b1]/[2×(b3–b4+b5)]),表示响应面沿不一致线横向位移的大小和方向(Atwater, Ostroff, Yammarino, & Fleenor, 1998)。负数表示结果与假设2一致。

**中介效应的检验。**对于假设3a和3b(即通过PJC传递对团队结果的一致性影响),我们遵循了Edwards和Cable(2009)提出的“块变量”方法。我们结合回归系数(见方程式1)得到加权线性组合(即块变量)。然后,我们计算块变量对中介变量PJC的回归系数,在中介模型中通常被称为“a”路径。接下来我们让中介变量和块变量对Y进行回归。中介变量对结果变量的回归系数代表“b”路径。我们对每一个结果都使用从这些分析中获得的系数来计算间接效应的估计值(a×b)。间接效应的显著性通过使用20000次Bootstrap构建的偏差校正的置信区间进行检验(Efron & Tibshirani, 1993)。
结果分析
这个部分虽然也很重要,但其中是一些数学语言,所以萜妹不会完全翻译,仅介绍关键部分。
结果分析包括三表一图,分别为:相关系数表、回归分析表、间接效应表和响应面图。相关系数表没什么不同,这里就不截图示意了。该部分先介绍回归分析表。
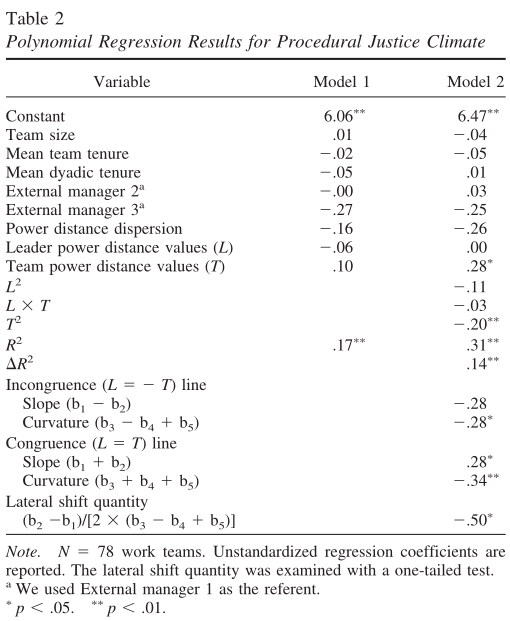

黄色部分为假设1的关键汇报指标。
- 二阶多项式中的△R2的显著增加,表明领导-团队权力距离值与PJC之间存在非线性关系;
- 不一致线的曲率为负且显著,满足第一个条件;
- 斜率p11和截距p10的置信区间都不包含0,说明和1/0无显著差别,满足第二个条件。
绿色下划线部分为对第三个条件的检验,不满足第三个条件,后续是对数据的解释。

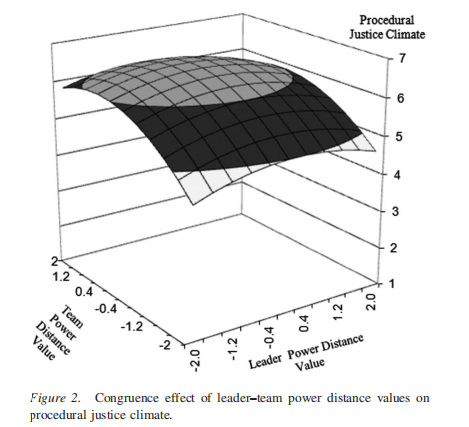
为了更全面地解释这些结果,我们使用系数估计来绘制图2中的整体响应面。沿不一致线的表面向下弯曲(凹面),意味着随着领导-团队权力距离变得更加一致,PJC的水平在增加;而随着领导-团队权力距离变得更加不一致(在任何一个方向),PJC的水平也在降低。如图所示,响应面的脊线不会明显偏离一致线。此外,沿一致线的曲面,PJC在中-中匹配时达到最高点。换言之,PJC随着领导与团队权力距离的完美契合(由于其正斜率)从低-低到中-中的增加而增加;然而,由于其负曲率,PJC随着领导与团队之间权力距离的完美匹配从中-中到高-高逐步降低。
上面这段一共五句话。第一句是交代响应面的构建;第二句交代了第一个条件满足的几何意义;第三句体现了第二个条件的满足;第四句则在不满足第三个条件的情况下,对一致性线的曲率和斜率进行解读;第五局是对上一句的扩展说明。

我们采用了单尾检验,因为我们的假设是有方向性的。横向位移量为负(=0.50, p<0.05),表明表面的转变向L<T的区域移动。

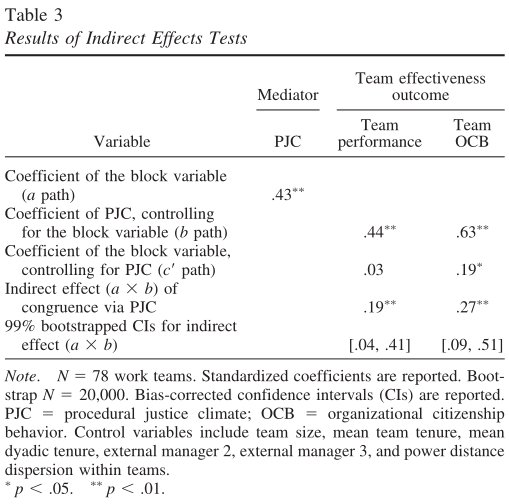
检验中介的部分和普通的中介检验并没有区别,这里就不展开说明啦。
啦啦啦,这篇文献的介绍就到这里啦。不知道小可爱们觉得怎么样。萜妹自认为还是有把它讲清楚的哦。
萜妹在介绍自己学方法的经验贴中有说过,遇到某些操作我拿不定的时候,我会去看些优质文献参考。我偶尔也会被小可爱问“XXX操作应该怎么处理呀?”、“有没有XXX方面的范文呀?”。所以这次想一鼓作气开开启新模块。
第一篇本来想做回复给我朋友的那篇文章,但是萜妹有半年没接触QCA了,所以稳妥点,还是先介绍我最有把握的这篇啦~
大家对这个模块有什么想法,以及有什么想看的范文可以留言和萜妹沟通哦。
另外,明天就是周更三周年了,到时候还会有篇总结推送。那小可爱们,明天见~
往期推送
原文链接
