共同方法偏差的综合分析策略
Williams, L. J., & McGonagle, A. K. (2016). Four Research Designs and a Comprehensive Analysis Strategy for Investigating Common Method Variance with Self-Report Measures Using Latent Variables. Journal of Business and Psychology, 31(3), 339-359. https://doi.org/10.1007/s10869-015-9422-9
今天继续来介绍共同方法偏差的检验,不记得的小可爱可以先回顾下四种共同方法偏差的检验方式。
总得来说,可以分为:
- Unmeasured Latent Method Construct,将所有测量题项附载到一个潜变量上;
- Marker Variables,对假定为 CMV 来源的变量的间接测量;
- Measured Cause Variables,对假定为 CMV 来源的变量的直接测量;
- Hybrid Method Variables Model,上述三种方法的混合。
概述
作者描述了一套可适用于前文所述四种设计的综合分析策略。


Phase 1a: Evaluate the Measurement Model
此阶段的目标是检验将潜变量与其指标联系起来的测量模型,确保潜变量具有足够的判别效度,并且潜变量及其指标具有理想的测量属性。这一阶段需要对使用的所有潜变量和它们的指标(包括通过自我汇报测量的控制变量、标记变量、测量原因变量)的CFA模型进行评估。
为了减少估计和收敛问题的发生,作者建议通过标准化潜变量(将每个因子的方差设为1)来实现识别,而不是将参考因子载荷设为1。对CFA结果的评估包括描述绝对拟合度的卡方值,以及关注相对拟合度的CFI、RMSEA和SRMR等(e.g., Kline, 2010)。值得注意的是,有人支持绝对拟合度和相对拟合度两种方法,尽管大多数研究人员更重视后者而非前者(e.g., West et al., 2012)。
如果模型被证明具有足够的拟合,应该检查所有潜变量之间的因子相关性。如果存在任何一组潜变量间的相关性大于0.8(Brown, 2006),研究人员应该删除其一或将多个潜变量合并。根据Anderson和Gerbing(1988)的建议,作者认为指标的残差协方差矩阵(Residual covariance matrix)也可以用于判断模型拟合度,并且在后续发现CMV时可能有助于理解。然而,这与允许指标残差之间的协方差/相关性不同,特别是当后者用于改善模型拟合度时(作者不建议这样做)。最后,应该使用每个指标的平方多重相关性(Squared multiple correlations ,即每个指标归因于其潜变量的方差量)来计算指标的信度是足够的(如标准化因子载荷为0.6时的平方多重相关性应大于0.36,Kline, 2010)。此外,应该计算每个潜变量的复合信度(Composite reliability )以证明每个潜变量都由其多个指标很好地表示(e.g., West et al., 2012)。
Phase 1b: Establish the Baseline Model
这个阶段的目标是建立一个基准模型,该模型将用于后续检验CMV效应的存在。基线模型的实现需要两个操作,作者没有将它们分成不同的步骤,因为它们可以同时实现。
第一,确定方法潜变量的含义
具体而言,对于标记变量和测量原因变量,需要通过因子载荷将方法潜变量与它们自己的指标和实质性潜变量的指标相连。这会导致一个解释问题,因为如果同时自由估计所有这些因子载荷,方法潜变量的含义将成为由方法指标和实质性指标所测量的内容的混合,方法潜变量的含义将变得模糊不清。这会损害对MFL(见下图)的解释,不清楚从这实质性指标中被"提取"的是哪种类型的变异。
上述问题可以通过在检查方法因子对实质性指标产生影响之前,固定方法潜变量与其自身指标的因子载荷和误差方差来轻松解决。
如果只有一个方法指标,为了实现模型识别,其因子载荷应该被固定为1,其误差方差为[(1-指标的信度)(指标的方差)](文中是这么写的,我并不确定两个括号之间应该是什么符号)。如果单个方法指标是由多个项目组成的,应该使用系数α作为信度的估计。
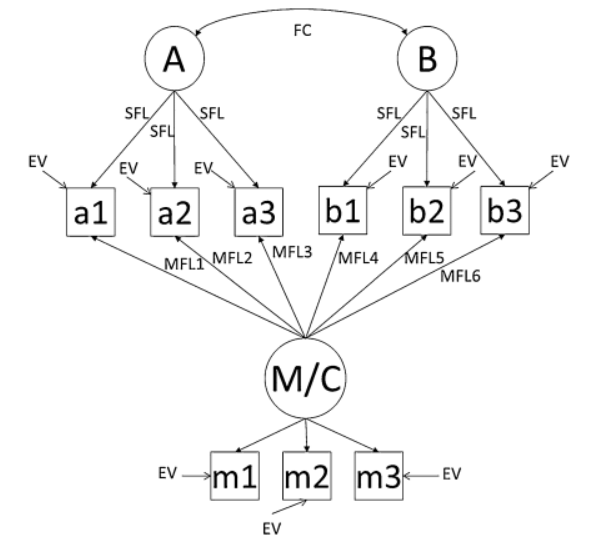
然而,如果使用多个指标来表示潜在的方法变量,则需要值来固定方法指标的多因素负载及其相关的误差方差。具体来说,从每个潜在的方法变量的CFA测量模型中保留未标准化的因子载荷和误差方差的估计,作为在建立基准模型时的固定参数使用。这些值是从在Phase 1a中检查的CFA测量模型中获得的,使用基于标准化潜变量(但未标准化指标)的模型结果。
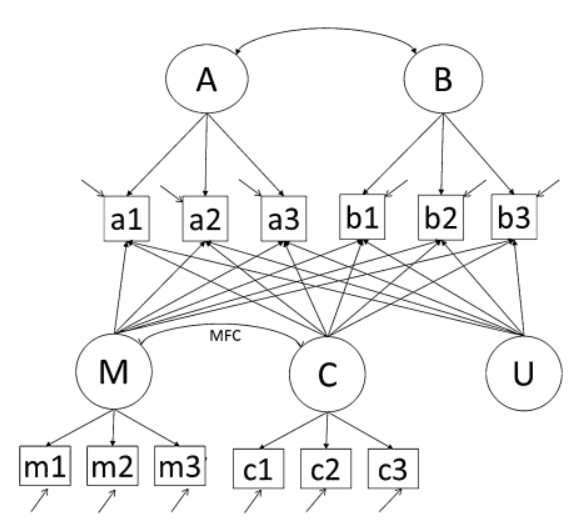
最后,由于ULMC方法因子没有自己的指标,在这一步骤中对它们唯一需要做的就是在基本测量模型中添加一个正交方法潜变量。
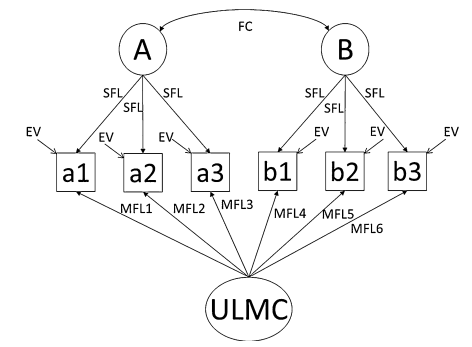
第二,方法潜变量均须与实质性潜变量正交
具体而言,基准模型假设每个方法潜变量与实质性潜变量不相关,但允许实质性潜变量彼此相关。将方法因子和实质性因子之间的相关性强制为零,可以简化在后续步骤中指标方差的划分。
对于混合设计,标记变量和测量原因变量可以相关,但每个方法变量必须与实质性潜变量和ULMC无关,以便实现识别。
最后,作者强调,测量模型和基线模型之间没有直接的模型比较。由于基线模型的限制性,可能会出现相对较差的拟合,只要初始的CFA测量模型显示出足够的拟合度,就可以进一步使用策略。
Phase 1c: Test for Presence and Equality of Method Effects
前两个阶段提供了关于潜变量及其指标的充分性的信息(Phase 1a),并建立了一个模型作为后续检验CMV的比较基准(Phase 1b)。
Phase 1c需要三个添加MFLs的附加模型(MethodU、MethodI、MethodC,使用三个步骤实现)以及使用卡方差异检验实现的一组关联的嵌套模型比较(e.g., Kline, 2010)。作者使用“Method”作为一个通用的标签,可以应用于任何类型的方法潜变量,并使用U、I和C作为下标的标签,以便讨论带有不同类型方法潜变量的混合模型。对于混合方法变量模型(Hybrid Method Variables Models),需要在下标的基础上添加一个额外的标签来表示潜变量的类型(U、M、C)。关于标识潜变量类型和MFLs相等性模式的完整描述见下表。
MethodU、MethodI和MethodC模型之间的一个关键区别是对实质性潜变量内部和之间的方法效果相等的假设。
第一步,基准模型和MethodU模型之间的卡方差异检验
MethodU模型基于Marker Variables / Measured Cause Variables Model 和Hybrid Method Variables Model,并包括将方法潜变量与实质性指标相连的在基准模型中被限制为零的MFLs(标记为MFL)。
在MethodU模型标签中,U代表“无限制”,指的是在该模型中,所有的MFLs都允许具有不同的值,并且可以自由估计。这个模型通常被称为研究共同性方法效应(Richardson et al., 2009)。
在Phase 1c的第1步中,如果基准模型和MethodU模型之间的卡方差异检验显著,意味着拒绝MFLs为零的假设,并得出了存在不相等的方法效应的初步结论。
第二步,MethodU和MethodI模型之间的卡方差异检验
如果保留了MethodU模型,研究人员将继续进行Phase 1c的第2步,其中包括检验MethodI模型。在MethodI模型中,将允许实质性因子之间的MFLs对实质性指标进行变化,但在这些因子内部将被约束为相等。换句话说,MFL1、MFL2和MFL3将被约束为相等,而MFL4、MFL5和MFL6将也被约束为相等,但MFL1与MFL4可以不同。
MethodU模型和MethodI模型是嵌套模型,因此使用卡方差异检验比较MethodI模型与MethodU模型的拟合度,并测试MFLs在因子内是否相等的假设。如果拒绝MethodI模型,意味着在实质性潜变量内存在不等的方法效应,并继续进行Phase 1d分析,使用MethodU的结果来测试实质性关系中的偏差。
第三步,MethodI和MethodC模型之间的卡方差异检验
如果保留MethodI模型并支持因子内相等的方法效应,则研究人员将继续测试本阶段的第三个模型(Phase 1c的第3步),即MethodC模型。
这个模型标签中的“C”反映了所有MFLs被约束为相等,即在实质性因子内部和跨实质性因子之间均相等。因此,这个模型被称为测试非共同性方法效应(Richardson et al., 2009)。在Phase 1c的第3步中,MethodI模型与MethodC模型的直接比较可以测试在实质性潜变量之间是否存在相等的方法效应。零假设是MFLs在实质性因子内部和之间都是相等的。如果得到的卡方差异超过相关自由度的临界卡方值,那么将拒绝实质性潜变量之间的CMV效应相等的零假设。在这种情况下,将暂时保留具有实质性潜变量内部相等约束的MethodI模型,并继续进行Phase 1d。如果卡方差异检验不显著,则保留MethodC模型,并得出结论认为在实质性潜变量内部和之间存在相等方法效应,并继续进行Phase 1d。
Phase 1d: Test for Common Method Bias in Substantive Relations
如果根据基准模型与MethodU、MethodI或MethodC模型的比较确定存在CMV,重点将转向在控制方法方差与不控制方法方差的模型中因子相关性的差异(即,是否受到CMV存在的偏倚)。在全面分析策略中,将基准模型的实质性因子相关性与MethodU、MethodI或MethodC模型(取决于Phase 1c中保留的模型)进行比较。
具体而言,研究人员进行两组因子相关性之间的整体统计差异测试。这个测试需要另一个模型,Method-R模型,其中“R”标签表示该模型对关键参数——实质性因子相关性进行了“限制”。在Method-R模型中,基准模型中的实质性因子相关性(在Phase 1b中)被输入为固定参数值,在该模型中,方法潜变量的指定由Phase 1c确定(同样是MethodU、MethodI或MethodC,取决于Phase 1c中保留的模型)。
如果测试结果显著,那么将拒绝因子相关性相等的零假设,并得出结论认为由于CMV存在,实质性因子相关性存在偏倚。如果模型比较测试支持存在偏倚,研究人员可以考虑实施其他Method-R模型,该模型一次只限制一个因素的相关性,以识别具体的偏倚情况。研究人员可能希望将特定的相关性测试限制在涉及关键的实质性模型外源变量和内源变量之间的关系,以避免进行过多的模型比较测试。如果进行了多个这样的测试,可以使用Bonferroni校正来调整显著性水平,以避免增加的I型错误率。
Phase 2a: Quantify Amount of Method Variance in Substantive Indicators
在(a)实质性指标和(b)实质性潜变量中量化CMV的存在也是很重要的。请注意,如果 Phase 1c 结果表明存在 CMV,研究人员应进行第 2a 阶段和第 2b 阶段,而无论在Phase 1d中是否发现了实质性相关性的偏倚,而无论在Phase 1c中方法方差效应是否被证明是不相等的(MethodU),在实质性因子之间但不在因子内部是不相等的(MethodI),还是在实质性因子内部和之间是相等的(MethodC)。
为了获得估计值,研究人员只需对将每个实质性指标与保留的 MethodC、MethodI 或 MethodU 模型中的相关实质性或方法因子联系起来的标准化因子载荷进行平方。对于每个实质性指标,都会进行这样的计算,而对于给定潜变量中的所有指标或研究中的所有实质性指标,通常会使用平均值或中位数来汇总结果。所有四种研究设计都可以遵循此过程,但如果包含多个相关的方法潜变量,则应根据最终保留的方法模型为每个方法潜变量单独计算每个指标的方差分配结果,而非跨不同的方法变量进行聚合。
Phase 2b: Quantify Amount of Method Variance in Substantive Latent Variables
考虑到CMV对潜变量测量的影响也很有价值。潜变量程序的一个重要优势是它们允许对所谓的组合信度进行估计(e.g., Bagozzi,1982)。这种组合信度估计被认为优于系数α,因为它对所涉及的项目的相等性做出了更少的限制性假设。Williams等(2010)描述了“可靠性分解”方法,以确定与正在检查的特定形式的方法方差相比,复合估计的可靠性所获得的值有多少是由于实质性方差。它可以看作是在潜变量水平上对方差进行划分,与前面在指标级别上所描述的类似。正如Williams等(2010)所指出的,总体、实质性和方法信度的方程式分别如下:
如果设计涉及使用多个相关的方法潜变量,则单独分解每个源的影响仍然是合适的,但由于方法潜变量之间的相互关联未在上述公式中考虑,结果不应跨方法潜变量进行聚合。
这篇推送就到这里啦。文章还剩最后的示例部分,萜妹想找篇用了这种检验方法且公开了数据的文章实际操作一下(如果我找的到的话),所以示例部分还要再等等。
另外,这篇文章萜妹是在签证排队的时候看完的。看的时候没觉得很复杂,可是写起推送来,又常常纠结于一些部分的翻译表达(我的水平问题)。所以如果对这篇文章很有兴趣的小可爱,建议回原文看看。
这篇推送就到这里啦。文章后面还有具体的分析策略与示例,今天肉眼可见的写不完了(这周已经工作60个小时了,人已经麻了),所以有兴趣的小可爱们可以先自己去看看。我预计一个月内更完后半部分。
